|
|
Nun wollen wir uns der interessanten Frage zuwenden, wie sich der Absorptionsgrad der Wärmestrahlung und damit die Erdtemperatur erhöhen, wenn sich die CO2-Konzentration in der Atmosphäre erhöht. Dazu soll, wie allgemein üblich, in einer Modellrechnung untersucht werden, welche Temperaturerhöhung durch eine Verdopplung der gegenwärtigen Konzentration von 380ppm hervorgerufen wird.
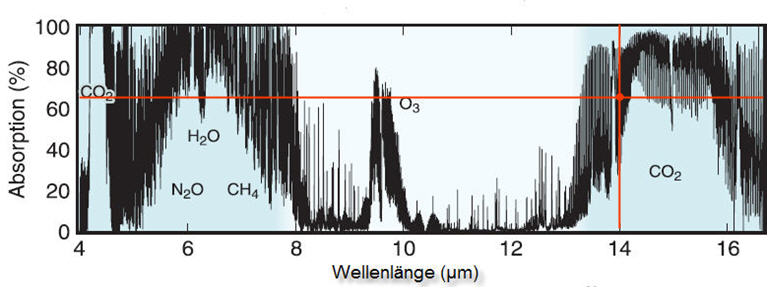
Abb. 11-1: Absorption der Infrarotstrahlung in der Atmosphäre, (Quelle: IPCC, Special Report on Safeguarding the Ozone and the Global Climate System, S.156)
In Abbildung 11-1 ist die Absorption der Infrarotstrahlung in der Atmosphäre nach Satellitenaufnahmen zu sehen. Die rechte helltürkis hervorgehobene Fläche stellt das 15μm Band der CO2-Deformationsschwingung dar. Dass dieser Bereich nicht völlig in der Sättigung ist, liegt daran, dass CO2 in großen Höhen also bei niedrigem Druck strahlen kann. Die freie Weglänge und damit die Zeit zwischen zwei Stößen werden dann so groß, dass Photonen nahezu ungehindert abgestrahlt werden können. Die Linie ist dann nicht mehr druckverbreitert sondern dopplerverbreitert. Bei genauem Hinschauen erkennt man, dass der gesättigte Bereich die Form eines Emissionsspektrums besitzt mit dem Q-Zweig im Zentrum.
Der CO2-infrarotaktive Bereich von 13μm bis 17μm entspricht einem Frequenzbereich von 17THz bis 23THz mit dem Zentrum bei 20THz. Nach den Abbildungen 6-3 und 9-2 besteht das Spektrum aus einem P-, Q- und R-Zweig. Man kann die Breite des P- und des R-Zweiges mit jeweils etwa 3THz ansetzten. Die Form der Zweige folgt als Rotationsschwingungsspektrum der Boltzmann-Statistik nach (4.14) und (11.1), wie sie in Abbildung 4-4 dargestellt ist.
| $$N_J = N_0 \cdot \left( {2 \cdot J + 1} \right) \cdot e^{ - \frac{{B_f \cdot h \cdot J \cdot \left( {J + 1} \right)}}{{k_B \cdot T}}} $$ |
(11.1) |
Wir wollen nun berechnen, wie viele Linien im angegebenen Bereich von 3THz pro Zweig aktiv sind. Die Rotationskonstante Bf beträgt nach (4.8) ca. 12GHz. Für die CO2-Deformationsschwingung liegt der Linienabstand wegen molekülinterner Symmetrieeffekte bei 4·Bf. Der Einfachheit halber rechnen wir bei der Modellrechnung konsequent mit einem Linienabstand von 2·Bf und können daher (11.1) unverändert benutzen. Für unsere Abschätzungen machen wir damit keinen Fehler. Die Anzahl der aktiven Linien n ergibt sich somit aus dem Quotienten der Zweigbreite bZweig und dem Linienabstand 2·Bf.
| $$n = \frac{{b_{Zweig} }}{{2 \cdot B_f }} = \frac{{3THz}}{{0,024THz}} = 125$$ |
(11.2) |
Im nächsten Schritt berechnen wir die statistische Anzahl der Moleküle der 125. Linie nach (11.1) bei einer fiktiven Annahme von N0=1 und einer Temperatur von +15°C.
| $$N_{125} = \left( {2 \cdot 125 + 1} \right) \cdot e^{ - \frac{{12GHz \cdot 6,626 \cdot 10^{ - 34} Js \cdot 125 \cdot \left( {125 + 1} \right)}}{{1,381 \cdot 10^{ - 23} \frac{J}{K} \cdot 288K}}} = 5,311 \cdot 10^{ - 12} $$ |
(11.3) |
Nun wird die CO2-Konzentration verdoppelt, indem N0=2 gesetzt wird. Damit muss sich auch die statistische Anzahl der Moleküle der 125. Linie nach (11.1) verdoppeln, so dass wir sofort schreiben können:
| $$N_{125}^/ = 2 \cdot N_{125} = 2 \cdot 5,311 \cdot 10^{ - 12} = 10,622 \cdot 10^{ - 12}$$ |
(11.4) |
Jetzt werden schrittweise neue Linien hinzugefügt, bis wieder die Anzahl N125 erreicht ist. Die Abnahme der statistischen Anzahl ist in Tabelle 11-1 dargestellt.
| N125’ |
N126’ |
N127’ |
| 10,622·10-12 |
6,469·10-12 |
3,924·10-12 |
Tab. 11-1: statistische Molekülanzahl bei 760ppm CO2 ab der 125. Linie
Nach nur zwei zusätzlichen Linien ist der Wert von (11.3) bereits deutlich unterschritten. Damit lässt sich der Breitenzuwachs des Spektrums einfach berechnen mit:
| $$\frac{{127}}{{125}} \cdot 100\% = 101,6\% $$ |
(11.5) |
Bei CO2-Konzentrationsverdopplung hat man also nur mit einem Breitenzuwachs des infrarotaktiven Bereichs von 1,6% zu erwarten. Setzt man in erster Näherung diesen Wert ins Verhältnis zum angegeben Treibhaustemperatureffekt des CO2 von 7,2°C nach Tabelle 2-1, so kommt man auf einen Temperaturanstieg von:
| $$1,016 \cdot 7,2^\circ C = 7,32^\circ C$$ |
(11.6) |
Nach dieser einfachen Abschätzung würde die CO2-Konzentrationverdopplung von gegenwärtig 380ppm auf 760ppm nur zu einem Temperaturanstieg um 0,12°C führen.
Als nächstes wollen wir im CO2-Absorptionsspektrum von Abbildung 11-1 graphisch die Wellenlänge bestimmen, bei dem die gemittelte Absorption der Wert 1-e-1 = 0,632 erreicht. Ab einer Absorption von 63,2% wird die Atmosphäre als optisch dicht bezeichnet. Die gesuchte Wellenlänge λ63% liegt bei etwa 14μm. Die zugehörige Frequenz f63% berechnet sich dann zu:
| $$f_{63\% } = \frac{c}{{\lambda _{63\% } }} = \frac{{300000000\frac{m}{s}}}{{14 \cdot 10^{ - 6} m}} = 21,43TH$$ |
(11.7) |
Da das Zentrum des Spektrums bei 20THz liegt, beträgt der Abstand vom Zentrum 1,43THz. Bei einem Linienabstand von 2·Bf ergibt das analog (11.2) folgende Linie:
| $$n_{63\% } = \frac{{f_{63\% } - f_0 }}{{2 \cdot B_f }} = \frac{{1,43THz}}{{0,024THz}} \approx 60$$ |
(11.8) |
Die 60. Linie markiert den Übergangspunkt zwischen optisch durchlässig und optisch dicht. In einer Excel-Simulation wurden nach (11.1) für N0=1 in einer ersten Spalte 150 Linien berechnet. Dann wurde in einer zweiten Spalte N0 verdoppelt. Der Wert der 60. Zeile in Spalte N0=1 entspricht somit der Konstanten für den Übergang optisch dicht nach optisch durchlässig. Sein Wert beträgt:
| $$N_{60} = 0,0832$$ |
(11.9) |
Nun wird nach dem Lambert-Beerschen Gesetz in der Form von (11.10) für jede Linie mit Hilfe der Konstanten von (11.9) die Absorption für beide Spalten berechnet (wobei bei J=60 die Bedingung 1-e-1 = 0,632 erfüllt wird).
| $$A(J) = 1 - e^{ - \frac{{N_J }}{{N_{60} }}} $$ |
(11.10) |
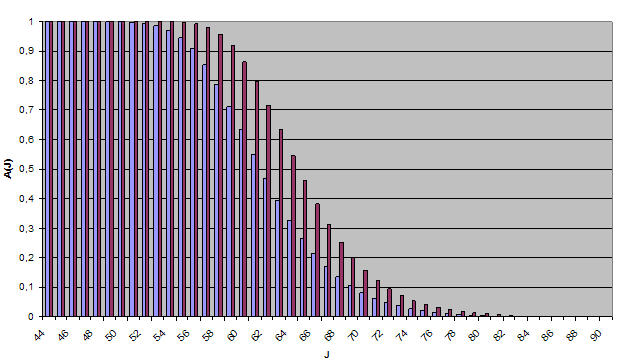
Abb. 11-2: Absorptionszuwachs bei Verdopplung der CO2-Konzentration
In Abbildung 11-2 ist der Ausschnitt im Spektrum dargestellt, in dem sich die Linien beider Spalten wesentlich unterscheiden. Im Rest des Spektrums sind sie durch die Wirkung der e-Funktion praktisch gleich. Die blauen Balken zeigen die Spalte N0=1 und die roten Balken die Spalte N0=2. Der Höhenunterschied in dem dargestellten Teil des Spektrums bestimmt den Zuwachs an Strahlungsenergieeintrag bei CO2-Konzentrationsverdopplung. Da sich nach Tabelle 11-1 der infrarotaktive Bereich des CO2 bis zur 127. Linie erstreckt, werden die Absorptionen aller Linien bis zur 127. Linie aufsummiert. Anschließend wird die erhaltene Summe durch die Linienanzahl dividiert. Das Ergebnis ergibt prozentual die Absorption im infrarotaktiven Bereich des CO2 von 17 bis 23μm. Die Simulation ergab folgende Werte:
| $$\frac{{\sum\limits_0^{127} {A_{N_0 = 1} (J)} }}{{128}} \cdot 100\% = 49,0\% $$ |
(11.11) |
| $$\frac{{\sum\limits_0^{127} {A_{N_0 = 2} (J)} }}{{128}} \cdot 100\% = 51,3\% $$ |
(11.12) |
Damit erhöht sich bei CO2-Konzentrationsverdopplung die Absorption im infrarotaktiven Bereich nur um 2,3%.
Nach (2.1) lässt sich die Strahlungsintensität der der Erde ohne Treibhauseffekt bei -18°C und mit Treibhauseffekt bei +15°C berechnen.
| $$I_{ - 18^\circ C} = \sigma \cdot T^4 = 5,67 \cdot 10^{ - 8} \frac{W}{{m^2 \cdot K^4 }} \cdot \left( {255K} \right)^4 = 240\frac{W}{{m^2 }}$$ |
(11.13) |
| $$I_{ + 15^\circ C} = \sigma \cdot T^4 = 5,67 \cdot 10^{ - 8} \frac{W}{{m^2 \cdot K^4 }} \cdot \left( {288K} \right)^4 = 390\frac{W}{{m^2 }}$$ |
(11.14) |
Durch den Treibhauseffekt werden also 150W/m2 bei +15°C an der Abstrahlung gehindert. Berechnet man analog (5.2) die Abstrahlung der Erde im Frequenzbereich von 17THz bis 23THz, so erhält man:
| $$\int\limits_{17THz}^{23THz} {\frac{{2 \cdot \pi \cdot h \cdot f^3 }}{{c^2 }} \cdot \frac{1}{{e^{\frac{{h \cdot f}}{{k_B \cdot T}}} - 1}} \cdot df} = 81,4\frac{W}{{m^2 }}$$ |
(11.15) |
Diese Berechnung wurde numerisch durchgeführt, da sie analytisch sehr kompliziert ist. Nach (11.11) wird in diesem Bereich aber 49% der Strahlung vom CO2 absorbiert:
| $$81,4\frac{W}{{m^2 }} \cdot 0,49 = 39,9\frac{W}{{m^2 }}$$ |
(11.16) |
Das ergibt bezogen auf die Gesamtabsorption von 150W/m2 einen Anteil von:
| $$\frac{{39,9\frac{W}{{m^2 }}}}{{150\frac{W}{{m^2 }}}} \cdot 100\% = 26,6\% $$ |
(11.17) |
Bezieht man den Wert von (11.17) auf die gesamte durch den Treibhauseffekt bedingte Temperaturerhöhung von 33K, so erhält man in erster Näherung einen CO2-bedingten Anteil von:
| $$33K \cdot 0,266 = 8,8K$$ |
(11.18) |
Verglichen mit der CO2-bedingten Temperaturerhöhung von 7,2K aus Tabelle 2-1, liegt der Wert von (11.18) etwas höher. In der vorliegenden Simulationsrechnung wurde aber nicht berücksichtigt, dass CO2 in großen Höhen strahlt und somit auch Energie abgeführt wird. Der nach (11.17) berechnete CO2-bedingte Anteil am Treibhauseffekt von ca. 25% wird in der Literatur auch so angegeben. Der eingeschlagene Rechenweg wird damit prinzipiell bestätigt.
Berechnet man nun die bei verdoppelter CO2-Konzentration in der Atmosphäre absorbierte Strahlungsleistung, so erhält man mit (11.12) analog (11.16):
| $$81,4\frac{W}{{m^2 }} \cdot 0,513 = 41,8\frac{W}{{m^2 }}$$ |
(11.19) |
Damit ergibt sich nach (11.16) und (11.19) eine Erhöhung der atmosphärisch absorbierten Energie um 1,9W/m2. Wegen des Strahlungsgleichgewichts muss sich die Temperatur der Erde erhöhen, um diesen Abstrahlungsverlust über die noch offenen Strahlungsfenster auszugleichen. Nach (11.14) kann die neue mittlere Erdtemperatur berechnet werden, wenn die gegenwärtig abgestrahlten 390W/m2 um die CO2-bedingten Absorptionsverluste von 1,9W/m2 korrigiert werden. Wie man in Abbildung 11-1 leicht sehen kann, reicht es nicht aus, die abgestrahlte Energie der Erde um die berechneten 1,9W/m2 zu erhöhen, da beispielsweise Wasserdampf in großen Frequenzbereichen ebenfalls eine Totalabsorption verursacht. Vielmehr müssen die 1,9W/m2 noch mit dem Treibhauseffekt bedingten Emissionsgrad der Erde εT analog (2.12) korrigiert werden. Der Emissionsgrad nach (2.12) entspricht aber dem Transmissionsfaktor nach (8.4) und damit auch dem Verhältnis von ausgestrahlter Leistung I-18°C zur eingestrahlten Leistung I+15°C. Nach (2.12), (8.4), (11.13) und (11.14) gilt:
| $$\varepsilon _T = \frac{{\left( {255K} \right)^4 }}{{\left( {288K} \right)^4 }} = \frac{{I_{ - 18^\circ C} }}{{I_{ + 15^\circ C} }} = \frac{{240\frac{W}{{m^2 }}}}{{390\frac{W}{{m^2 }}}} = 0,615$$ |
(11.20) |
Mit Gleichung (11.20) wird der aktuelle Emissionsgrad ermittelt. Mit der erhöhten Absorption bei CO2-Konzentrationsverdopplung muss sich εT entsprechend verringern. Analog (11.20) lässt sich der neue Emissionsgrad εTn wie folgt bestimmen:
| $$\varepsilon _{Tn} = \frac{{I_{ - 18^\circ C} }}{{I_n }} = \frac{{\sigma \cdot \left( {255K} \right)^4 }}{{\sigma \cdot T_n^4 }} = \frac{{\left( {255K} \right)^4 }}{{T_n^4 }}$$ |
(11.21) |
Damit ergibt sich zur Berechnung der neuen mittleren Erdtemperatur Tn folgende Beziehung:
| $$\sigma \cdot T_n^4 = I_{ + 15^\circ C} + \frac{{1,9\frac{W}{{m^2 }}}}{{\varepsilon _{Tn} }} = 390\frac{W}{{m^2 }} + \frac{{1,9\frac{W}{{m^2 }}}}{{\frac{{\left( {255K} \right)^4 }}{{T_n^4 }}}} = 390\frac{W}{{m^2 }} + \frac{{1,9\frac{W}{{m^2 }}}}{{\left( {255K} \right)^4 }} \cdot T_n^4 $$ |
(11.22) |
Gleichung (11.22) wird nun durch σ dividiert und anschließend nach Tn umgestellt:
| $$T_n^4 = \frac{{390\frac{W}{{m^2 }}}}{\sigma } + \frac{{1,9\frac{W}{{m^2 }}}}{{\sigma \cdot \left( {255K} \right)^4 }} \cdot T_n^4 = \left( {288K} \right)^4 + \left( {\frac{{76K}}{{255K}}} \right)^4 \cdot T_n^4 = \left( {288K} \right)^4 + \left( {0,298} \right)^4 \cdot T_n^4 $$ |
|
| $$T_n^4 = \frac{{\left( {288K} \right)^4 }}{{0,992}}$$ |
→ |
$$T_n = \frac{{288K}}{{\sqrt[4]{{0,992}}}} = 288,6K$$ |
(11.23) |
Damit ergibt sich eine mittlere Temperaturerhöhung bei CO2-Konzentrationsverdopplung von gegenwärtig 380ppm auf 760ppm von ca.:
| $$288,6K - 288K = 0,6K$$ |
(11.24) |
Der neue Emissionsgrad εTn berechnet sich nach (11.21) und (11.23) zu:
| $$\varepsilon _{Tn} = \frac{{\left( {255K} \right)^4 }}{{\left( {288,6K} \right)^4 }} = 0,609$$ |
(11.25) |
Verglichen mit den Modellunterschieden von Tabelle 2-2, könnte man das Absenken von εT um 0,006 noch als im Rahmen von Rechenungenauigkeiten liegend bezeichnen. Auch das Ansteigen der mittleren Erdtemperatur um 0,6°C nach (11.24) bei Verdopplung der gegenwärtigen CO2-Konzentration braucht in Anbetracht der jährlichen Schwankungen bei uns nicht die geringste Besorgnis auszulösen.
Dass dem CO2 bei der Erhöhung des Treibhauseffekts eine größere Rolle zugemessen wird, als ihm eigentlich zukommt, wird auch von den Befürwortern der CO2-Reduktion zugegeben. So heißt es beispielsweise in der Schrift "Der Klimawandel – Eine aktuelle Bilanz globaler Prozesse und ihrer regionalen Folgen" (Alexander Siegmund, online veröffentlicht am 4.03.2008, Springer-Verlag, Heidelberg, DOI 10.1007/s00550-008-0068-1):
"Neben der Lage und Sättigung der Absorptionsspektren spielen auch das Ausmaß der Konzentrationsveränderungen, das spezifische Treibhauspotenzial im Vergleich zum Kohlendioxyd und die mittlere atmosphärische Verweilzeit eine wichtige Rolle für den Einfluss der einzelnen Spurengase auf den zusätzlichen, anthropogenen Treibhauseffekt. Dabei kommt v. a. dem Methan, Ozon und Distickstoffoxid, das vor allem durch den zunehmenden Kunstdüngereinsatz in der Landwirtschaft in starkem Maße emittiert wird, eine wichtige Bedeutung zu. Die Absorptionsbanden dieser Spurengase sind zumeist noch ungesättigt und bergen daher bei einem weiteren Konzentrationsanstieg in der Atmosphäre noch ein erhebliches Treibhauspotenzial in sich (vgl. u. a. Enquete-Kommission 1995). Anders beim Kohlendioxyd. Durch die weitgehend gesättigten Banden nimmt das Treibhauspotential zusätzlicher CO2-Moleküle nur noch logarithmisch zur Konzentration des Gases zu. Dennoch kommt dem CO2 eine zentrale Funktion für den anthropogenen Treibhauseffekt zu – allein 2004 sind die Emissionen weltweit um 4,5% gestiegen, 2005 noch 2,5%, wodurch die CO2-Konzentration derzeit jährlich um etwa 2,5ppm steigt (vgl. endlicher 2007)." (Hervorhebung vom Autor)
Im Klartext heißt das, dass bei einem weiteren Anstieg der CO2-Konzentration der Treibhauseffekt zwar nur marginal (logarithmisch) zunimmt, aber das der Anstieg schon um des Anstiegs Willen kritisch ist und daher begrenzt werden muss.
Einen ähnlich geringen Wert für die Temperaturerhöhung bei CO2-Konzentrationsverdopplung wie in (11.24) nennt auch Professor Rahmstorf vom Potsdam Institut für Klimafolgenforschung (kurz PIK) in seinem Buch "Der Klimawandel" (Rahmstorf/Schellnhuber, Verlag C. H. Beck, München, 6. Auflage, 2007, S.42):
"Man kann von der Physik ausgehen, nämlich von der im Labor gemessenen Strahlungswirkung von CO2, die ohne jede Rückkopplung direkt eine Erwärmung um 1,2°C bei einer Verdoppelung der Konzentration bewirken würde. Dann muss man noch die Rückkopplungen im Klimasystem berücksichtigen: Im Wesentlichen Wasserdampf, Eis-Albedo und Wolken."
Das PIK ist ein starker Befürworter für sofortige Maßnamen zur Reduktion vom CO2-Ausstoß und damit für einen völligen Umbau unserer Wirtschaft und damit auch Gesellschaft. Er tritt auch immer wieder mit Streitschriften gegen so genannte Klimaleugner an die Öffentlichkeit. Aber ganz so sicher ist er sich mit der Temperaturerhöhung um 1,2°C auch nicht. In seiner Schrift "Antwort auf Mangini's Artikel – Ihr kennt die Gründe nicht" (zu finden auf seiner PIK-Homepage) schreibt er zu dem Thema:
"Ebenso unumstritten ist die Tatsache, dass CO2 die Strahlungsbilanz der Erde verändert. Der direkte Effekt einer CO2-Verdoppelung wäre eine Erwärmung um 1°C - dies ist seit dem 19. Jahrhundert bekannt und leicht nachzurechnen. Die Unsicherheit, wie stark die tatsächliche Erwärmung letztlich sein wird, kommt von den Rückkopplungen im Klimasystem. Diese können die Erwärmung verstärken (wenn etwa durch die Erwärmung mehr Wasserdampf in die Atmosphäre gelangt), sie könnten sie aber auch abschwächen (wenn z.B. kühlende Wolken zunehmen). Die Klimageschichte gibt wertvolle Hinweise über die Wirkung dieser Rückkopplungen: Wären vergangene Klimaschwankungen immer sehr klein gewesen, wäre dies ein Indiz für abschwächende Rückkopplungen - dann würde auch ich zweifeln, ob unser CO2 das Klima aus dem Gleichgewicht bringen kann."
Man könnte auch etwas hinterhältig vermuten, dass die 0,6°C (in der Literatur werden auch 0,7°C genannt) großzügig auf 1°C aufgerundet worden sind. Auf alle Fälle ist der physikalisch nachvollziehbare Wert der Temperaturerhöhung selbst für Professor Rahmstorf zu gering, um für sich allein genommen eine Klimapanik auslösen zu können. Daher müssen verstärkende Faktoren bzw. positive Rückkopplungen gefunden werden, um publikumswirksam zu Erhöhungen um 5...10°C zu kommen. Diese Rückkopplungseffekte sollen uns im nächsten Kapitel beschäftigen.
|


