
Edward Bernays, "Propaganda", H. Liveright, 1928
6. Der rotierende Oszillator
|
Home Kapitel 5 Kapitel 7 Download Kapitel 6 Impressum
|
Da die zur Anregung der Rotation notwendige Energie viel niedriger ist als die zur Anregung der Schwingung, wird ein schwingendes Molekül allgemein auch rotieren. Man kann Moleküle in diesem Zustand auch als rotierenden Oszillator bezeichnen. In erster Näherung kann man die Anregung des Moleküls einfach als die Summe der Anregungen des harmonischen Oszillators und des starren Rotators betrachten. Für die Energieniveaus erhält man somit:
| $$E(V,J) = E_{vib} (V) + E_{rot} (J) = h \cdot f_0 \cdot \left( {V + \frac{1}{2}} \right) + B_f \cdot h \cdot J \cdot \left( {J + 1} \right)$$ | (6.1) |
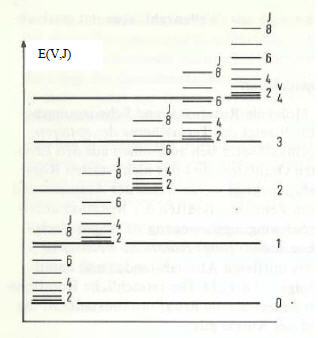
Abb. 6-1: Energieniveaus des rotierenden Oszillators (© Wiley-VCH Verlag GmbH & Co. KGaA)
Wenn die Anregungsenergie für die Schwingung gering ist, können wie in Abbildung 6-1 die höheren Rotationsniveaus mehr Energie aufnehmen als der nächst höher angeregte Schwingungszustand. Beim CO2-Molekül ist das aber nicht der Fall.
In Abbildung 6-1 nehmen die Abstände der einzelnen Schwingungsniveaus zu höheren V hin ab. Das liegt daran, dass sich das Modell des harmonischen Oszillators streng genommen nur auf die untersten Schwingungsniveaus anwenden lässt. Die durch die Bindungskräfte modellhaft dargestellte Feder lässt sich nicht beliebig stauchen und nach außen hin brechen die Bindungskräfte auseinander, wenn die Schwingung zu stark wird. Diese Grenze wird Dissoziationsenergie genannt. Da die Energieniveaus nicht mehr genau äquidistant sind, kommt es zu so genannten Oberschwingungen die ungefähr bei der doppelten, dreifachen usw. Frequenz der Grundschwingung liegen. Sie werden in Anlehnung an die Akustik auch als Obertöne bezeichnet. In unserem Fall ist aber nur das erste Schwingungsniveau geringfügig thermisch angeregt, so dass die Obertöne des CO2 bei der mittleren Erdtemperatur von +15°C nicht ins Gewicht fallen.
Bei einem Schwingungsübergang V0→1 und umgekehrt kann sich die Rotationsquantenzahl J nur um ±1 ändern. Das heißt, der mit einem Schwingungsübergang verbundene Rotationsquantensprung kann nur in den nächst höheren bzw. niedrigeren Energiezustand erfolgen. Im Fall der Deformationsschwingung des CO2 ist auch der direkte Übergang auf das nächste Schwingungsniveau ohne Änderung der Rotationsquantenzahl erlaubt, während das bei der asymmetrischen Streckschwingung nicht der Fall ist.
Wegen der Koppelung der Schwingung mit der Rotation kann ein Teil der Rotationsenergie für den Übergang zum höheren Schwingungsniveau genutzt werden, die dazu nötige Frequenz der elektromagnetischen Strahlung ist dann um die Rotationsenergie niedriger. Genauso umgekehrt kann eine höhere Frequenz, als zum Schwingungsübergang notwendig, zur Erhöhung der Rotationsgeschwindigkeit führen. Das Ergebnis ist eine Projektion des Rotationsspektrums links und rechts vom Zentrum des reinen Schwingungsübergangs (wenn erlaubt). Die Serie bzw. Bande mit ΔJ=+1 wird als R-Zweig und die mit ΔJ=-1 als P-Zweig bezeichnet. Der reine Schwingungsübergang in der Mitte zwischen R- und P-Zweig ist der Q-Zweig.
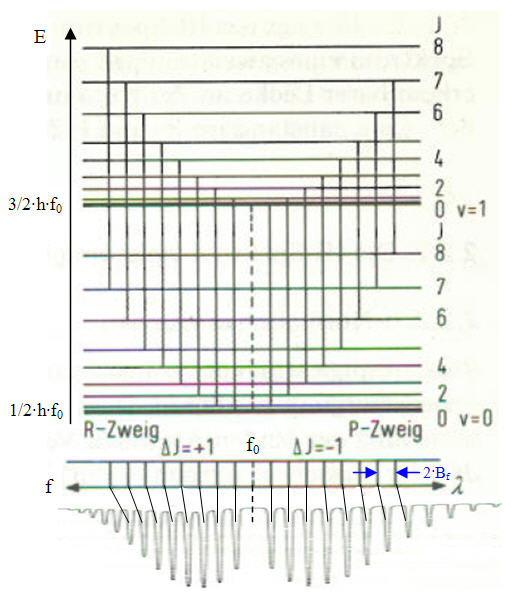
Abb. 6-2: Rotationsschwingungsspektrum von HCl (© Wiley-VCH Verlag GmbH & Co. KGaA)
In Abbildung 6-2 (Quelle: Günzler/Böck, "IR-Spektroskopie", Verlag Chemie GmbH, Weinheim, 1975, S.25) ist als Beispiel das Rotationsschwingungsspektrum des zweiatomigen heteronuklearen Moleküls HCl dargestellt. Der Q-Zweig des reinen Schwingungsübergangs ist hier nicht erlaubt. Im oberen Teil der Abbildung sieht man die Verbindung eines Rotationsübergangs in Verbindung mit dem Schwingungsübergang wobei nur ΔJ±1 für die Rotationsquantenzahl erlaubt ist. Die Schwingungsquantenzahl V ändert sich nur von 0→1. Man erkennt den Linienabstand von 2·B und die nach einer e-Funktion auslaufenden Flanken des Spektrums analog dem Rotationsspektrum von Abbildung 4-4. Durch die Schwingung wird das Rotationsspektrum gleichsam um die Eigenfrequenz f0 gespiegelt und im Frequenzbereich nach oben transformiert.
Im unteren Teil der Abbildung 6-2 ist das Spektrum von HCl dargestellt. Wenn man sich das Spektrum genau ansieht, so erkennt man, dass der R-Zweig etwas gestaucht und der P-Zweig etwas gestreckt erscheint. Das liegt daran, dass Schwingung und Rotation nicht wechselwirkungsfrei gleichzeitig erfolgen. Für die Rahmen dieser Arbeit gemachten Abschätzungen soll dieser Effekt jedoch vernachlässigt werden. Die einzelnen Linien ergeben sich nach (6.1) aus der Subtraktion benachbarter Zustände, wobei jeder Zustand eine Kombination von Schwingung und Rotation darstellt.
| $$f = f_0 \pm 2 \cdot B_f \cdot \left( {J + 1} \right)$$ | (6.2) |
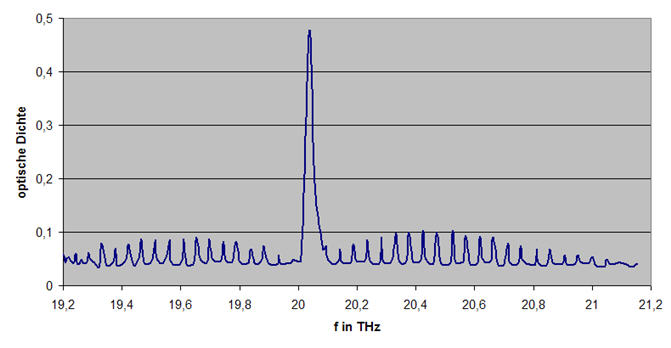
Abb. 6-3: Rotationsschwingungsspektrum von CO2 (Deformationsschwingung)
(Diagrammdaten: Haken/Wolf, "Molekülphysik und Quantenchemie", Springer Verlag, Heidelberg, 1991, S.172)
Bei der Deformationsschwingung gibt es noch die Besonderheit, dass auf Grund von Symmetrieeigenschaften des CO2-Moleküls jedes zweite Rotationsniveau nicht realisiert ist. Daher beträgt der Linienabstand bei der Deformationsschwingung 4·Bf anstatt 2·Bf wie bei der asymmetrischen Streckschwingung.
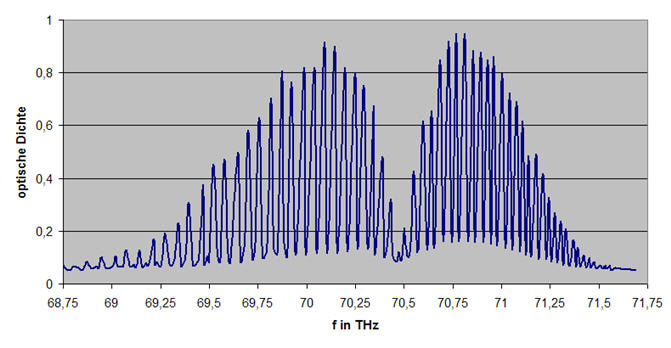
Abb. 6-4: Rotationsschwingungsspektrum von CO2 (asymmetrische Streckschwingung)
(Diagrammdaten: Haken/Wolf, "Molekülphysik und Quantenchemie", Springer Verlag, Heidelberg, 1991, S.172)
Wenn man die Anzahl der Linien zwischen 20,4 und 21,0THz auszählt, so erhält man 13 Linien. Damit lässt sich die Rotationskonstante Bf annähernd bestimmen:
| $$\Delta f = 4 \cdot B_f = \frac{{600GHz}}{{13}} = 46,15GHz$$ | → | $$B_f = 11,54GHz$$ | (6.3) |