3. Die Wärmekapazität der Luft

Der Treibhauseffekt geht davon aus, dass die Atmosphäre Strahlungsenergie aufnehmen, speichern und auch wieder abgeben kann. Energie wird in Gasen in Form ihrer inneren Energie U gespeichert. Dazu gehört zu allererst die ungeordnete Teilchenbewegung in den drei Dimensionen des Raumes. Hier wird von den drei Freiheitsgraden der Translation gesprochen. Ein einatomiges ideales Gas besitzt nur diese drei Freiheitsgrade. Allgemein berechnet sich die innere Energie U eines Gases:

$$U = \frac{f}{2} \cdot N \cdot k_B \cdot T$$

(3.1)

• f:	Anzahl der Freiheitsgrade
• N:	Teilchenanzahl
• kB:	Boltzmannkonstante (1,38·10-23J/K)
• T:	absolute Temperatur in Kelvin

Besteht das Gas aber aus Molekülen, so kommen noch weitere Freiheitsgrade der Rotation und der Vibration (Schwingung) hinzu. Ein zweiatomiges Molekül, wie z.B. molekularer Stickstoff oder Sauerstoff, besitzt insgesamt sechs Freiheitsgrade: drei der Translation, zwei der Rotation (Rotation um die Molekülachse ist aus quantenmechanischen Gründen nur für sehr hohe Energien möglich, so dass die zur Verfügung stehende thermische Energie nicht mehr ausreicht) und einen Schwingungsfreiheitsgrad. Dieser zählt allerdings bei der Berechnung der inneren Energie doppelt, weil er kinetische und potentielle Energie enthält. Rotations- und Schwingungsenergie sind quantisiert. Bei geringer Gesamtenergie eines Moleküls können energetisch höher liegende Rotations- und Schwingungsfreiheitsgrade nicht angeregt werden. Sie sind sozusagen "eingefroren". Deshalb verhalten sich die meisten zweiatomigen Gase wie zum Beispiel Wasserstoff, Sauerstoff oder Stickstoff unter Normalbedingungen (T=0°C; p=1013,25hPa) effektiv so, als hätten die Einzelmoleküle nur fünf Freiheitsgrade. Bei hohen Temperaturen sind dem System dagegen alle Freiheitsgrade offen.

Jedes Molekül hat 3·n (n = Anzahl der Atome im Molekül) Freiheitsgrade, weil man für jedes Atom drei Koordinaten braucht um seine Position zu definieren. Diese teilen sich bei den verschiedenen Molekülarten folgendermaßen auf:

n-atomig linear (z.B. N2, O2, CO2):

• Translationsfreiheitsgrade:	3
• Rotationsfreiheitsgrade:	2
• Schwingungsfreiheitsgrade (zählen bei der Berechnung der inneren Energie doppelt):	3·n-5

n-atomig nicht linear (z.B. H2O):

• Translationsfreiheitsgrade:	3
• Rotationsfreiheitsgrade:	3
• Schwingungsfreiheitsgrade (zählen bei der Berechnung der inneren Energie doppelt):	3·n-6

Das "Einfrieren" des Schwingungsfreiheitsgrades lässt sich sehr schön am Verhalten der spezifischen Wärmekapazität von trockener Luft in Abhängigkeit von der Temperatur zeigen. Die spezifische Wärmekapazität eines Stoffes ist eine physikalische Eigenschaft und bezeichnet die auf die Masse bezogene Wärmekapazität. Sie gibt an, welche Wärmemenge (gemessen in Joule) einem Stoff zugeführt werden muss, um seine Temperatur um ein Kelvin zu erhöhen. Für Gase werden zwei spezifische Wärmekapazitäten angegeben, eine bei konstantem Druck (isobar) cp und eine bei konstantem Volumen (isochor) cv, wobei cp > cv ist. Das kommt daher, dass bei isochoren Zustandsänderungen die zugeführte Wärmemenge komplett zur Erhöhung der Temperatur des Gases (also zur Erhöhung der kinetischen Energie der Gasteilchen) beiträgt. Bei isobaren Prozessen hingegen muss Volumenarbeit verrichtet werden, da sich das Gas beim Erwärmen ausdehnen muss, wenn der Druck konstant bleiben soll. Bei konstantem Druck wird daher ein Teil der zugeführten Wärmeenergie in Form von Volumenarbeit "verbraucht", weswegen mehr Wärmeenergie zugeführt werden muss, um ein Gas um ein Grad zu erwärmen, als bei isochoren Zustandsänderungen. Da sich erwärmte Luft in der Atmosphäre nahezu ungehindert ausbreiten kann, gilt hier cp. Die beiden spezifischen Wärmekapazitäten hängen folgendermaßen zusammen:

$$c_p - c_v = R_s = \frac{R}{M}$$

(3.2)

Hierbei ist Rs die spezifische Gaskonstante, R die allgemeine Gaskonstante und M die molare Masse. Weiterhin gilt in guter Näherung:

$$c_v = \frac{f}{2} \cdot R_s $$

(3.3)

Wobei f wieder die Anzahl der Freiheitsgrade ist. Ersetzt man in (3.2) cv durch (3.3) und teilt f in ftrans, frot und fvib auf, so erhält man für die isobare spezifische Wärmekapazität cp:

$$c_p = R_s + \frac{{f_{trans} + f_{rot} + 2 \cdot f_{vib} }}{2} \cdot R_s = R_s \cdot \left( {1 + \frac{{f_{trans} + f_{rot} + 2 \cdot f_{vib} }}{2}} \right)$$

(3.4)

Die spezifische Gaskonstante von trockener Luft beträgt:

$$R_s = 0,28706\frac{{kJ}}{{kg \cdot K}}$$

Nun kann cp für trockene Luft aus (3.4) berechnet werden, einmal mit und einmal ohne Berücksichtigung der Molekülschwingungen. Da Luft zu über 99% aus 2-atomigen Molekülen besteht, wird nur ein Freiheitsgrad für die Schwingung angesetzt.

• cp ohne Schwingung:	$$c_p = 0,28706\frac{{kJ}}{{kg \cdot K}} \cdot \left( {1 + \frac{{3 + 2}}{2}} \right) = 1,00447\frac{{kJ}}{{kg \cdot K}}$$
• cp mit Schwingung:	$$c_p = 0,28706\frac{{kJ}}{{kg \cdot K}} \cdot \left( {1 + \frac{{3 + 2 + 2 \cdot 1}}{2}} \right) = 1,29177\frac{{kJ}}{{kg \cdot K}}$$

In Abbildung 3-1 sieht man, dass bei niedrigen Temperaturen die Moleküle der Atmosphäre nicht oder nur in geringer Anzahl schwingen. Erst ab ca. +50°C reicht die thermische Energie aus, um Schwingungen anzuregen. In der Folge beginnt die spezifische Wärmekapazität bis zu einem Sättigungswert zu steigen, bei dem alle Moleküle zur Schwingung angeregt sind.

   
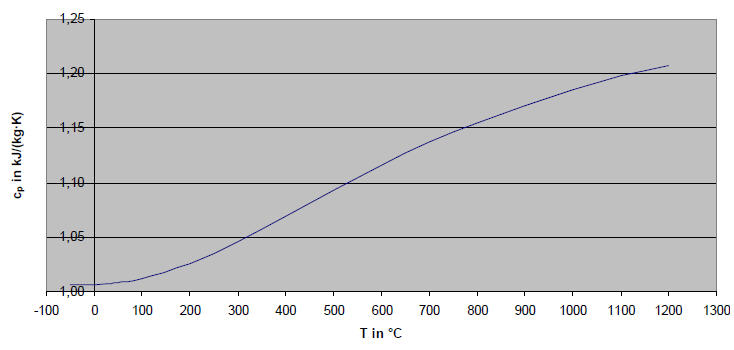
   Abb. 3-1: spezifische Wärmekapazität von Luft bei konstantem Luftdruck von 1bar