4. Rotation von Molekülen

Wie schon in Kapitel 3 beschrieben, kann ein Molekül auf verschiedene Weise Bewegungsenergie aufnehmen. Während die Translation als ungequantelte Wärmebewegung in Erscheinung tritt, führen Rotation und Vibration zu diskontinuierlichen Änderungen des Energiezustandes der Moleküle. Die Zahl der Rotationsfreiheitsgrade eines Moleküls hängt von seinem geometrischen Bau ab. Liegen alle Atomkerne des Moleküls hintereinander auf einer Linie, so spricht man von einem linearen Molekül. Solch ein Molekül kann nur um die zwei Achsen senkrecht zur Bindungsachse rotieren. Die Rotation um die Bindungsachse selbst ist wegen des zu geringen Trägheitsmoments nicht möglich. Ein lineares Molekül hat also zwei Freiheitsgrade der Rotation. Alle zweiatomigen Moleküle, wie z.B. die Hauptbestandteile der Atmosphäre N2 und O2, sind lineare Moleküle. Auch das CO2 mit seinen drei Atomkernen ist ein lineares Molekül. Nichtlineare Moleküle müssen aus mindestens drei winklig zueinander angeordneten Atomkernen bestehen. Auf Grund ihrer Masseverteilung können diese Moleküle um alle drei Achsen im Raum rotieren und haben daher auch drei Freiheitsgrade der Rotation. Ein Beispiel für ein nichtlineares Molekül ist H2O, dessen zwei Wasserstoffatomkerne mit dem Sauerstoffatomkern einen Winkel von 105° einschließen.

Am einfachsten wird die Rotationsbewegung mit dem Modell des starren Rotators beschrieben, bei dem das Molekül mit konstanten Atomkernabständen um seinen Schwerpunkt kreiselt. Die Rotationsenergie berechnet sich nach der Gleichung:

$$E_{rot} = \frac{1}{2} \cdot I \cdot \omega ^2 $$

(4.1)

Dabei ist I das Trägheitsmoment um die Rotationsachse und ω = 2·π·f die Winkelgeschwindigkeit der Rotationsbewegung (f entspricht der Frequenz oder Drehzahl). Das Trägheitsmoment I bezogen auf den Schwerpunkt S beträgt:

$$I = \sum {m_i \cdot R_i^2 } $$

(4.2)

Wobei mi die Masse eines an der Rotation beteiligten Atomkerns ist und Ri seinen Abstand zum Schwerpunkt darstellt.

   
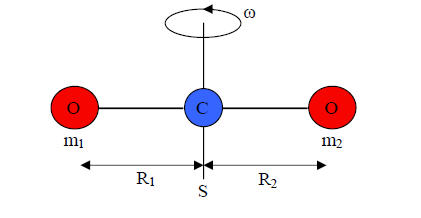
   Abb. 4-1: Rotation von CO2 um seinen Schwerpunkt

Da CO2 ein symmetrisch lineares Molekül ist, liegt sein Schwerpunkt im Kohlenstoffatomkern. Der Durchmesser des Kohlenstoffatomkerns ist klein gegenüber den Bindungsabständen zu den Sauerstoffatomkernen, deshalb braucht seine Masse nicht berücksichtigt werden. Nach dem Buch "Molekülphysik und Quantenchemie" (Haken/Wolf, Springer-Verlag, Heidelberg, 1991, S.15) betragen die Abstände R1 und R2 jeweils 1,15·10^-10m (siehe Abbildung 4-1). Die relative Atommasse von Sauerstoff wird dem Periodensystem der Elemente entnommen und beträgt 16. Um zur absoluten Masse des Sauerstoffatoms zu gelangen, muss seine relative Masse mit der atomaren Masse u = 1,6606·10^-27kg multipliziert werden.

$$m_O = 16 \cdot u = 16 \cdot 1.6606 \cdot 10^{ - 27} kg = 2.657 \cdot 10^{ - 26} kg$$

Nach (4.3) berechnet sich das Trägheitsmoment zu:

$$I_{CO_2 } = 2 \cdot m_O \cdot R_{C - O}^2 = 2 \cdot 2.657 \cdot 10^{ - 26} kg \cdot \left( {1.15 \cdot 10^{ - 10} m} \right)^2 = 7.0278 \cdot 10^{ - 46} kgm^2 = 7.0278 \cdot 10^{ - 46} Js^2 $$

(4.3)

Da Moleküle Rotationsenergie nur in diskreten Energiesprüngen (Quanten) aufnehmen können, kann (4.1) nicht direkt zur Berechnung der Rotationsenergie verwendet werden. Nach "Molekülphysik und Quantenchemie" (Haken/Wolf, Springer-Verlag, Heidelberg, 1991, S.138 ff) lautet die Quantenbeziehung für die Energieeigenwerte der Rotation:

$$E_{rot} = \frac{{h^2 }}{{8 \cdot \pi ^2 \cdot I}} \cdot J \cdot \left( {J + 1} \right)$$

$$J = 0,1,2,3,...$$

(4.4)

Dabei ist h = 6,6261·10^-34Js das Plancksche Wirkungsquantum und J die Rotationsquantenzahl, mit der die einzelnen diskreten Rotationsniveaus durchnummeriert werden. Mit Einführung der molekülabhängigen Rotationskonstanten Bf wird aus (4.4):

$$E_{rot} = B_f \cdot h \cdot J \cdot \left( {J + 1} \right) = B_f \cdot h \cdot \left( {J^2 + J} \right)$$

(4.5)

Die Rotationsenergie steigt also quadratisch mit Quantenzahl an.

   
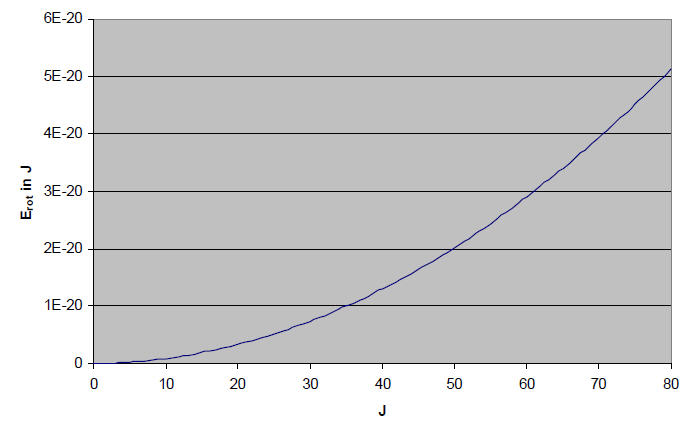
   Abb. 4-2: Energieniveaus von CO2

In Abbildung 4-2 wird der Verlauf der Energiezunahme in Abhängigkeit von J dargestellt, wobei für J nur diskrete Werte zugelassen sind. Normalerweise wird die Rotationskonstante B in der Spektroskopie mit der Wellenzahl in cm^-1 angegeben. Im Rahmen dieser Schrift soll sie jedoch der einfacheren Verständlichkeit halber in der Einheit Hz als Bf geschrieben werden. Die Konstanten B und Bf sind über die Lichtgeschwindigkeit c folgendermaßen miteinander verknüpft:

$$B = \frac{{B_f }}{c}$$

(4.6)

Die Rotationskonstante hat in der Spektroskopie eine große Bedeutung. Ihr Wert kann direkt aus einem Spektrum abgelesen werden, da er in unmittelbarer Beziehung zu den Linienabständen steht. Aus der Rotationskonstante kann man Rückschlüsse auf den inneren Aufbau eines Moleküls ziehen. Nach (4.4) und (4.5) lautet ihre Formel:

$$B_f = \frac{h}{{8 \cdot \pi ^2 \cdot I}}$$

(4.7)

Setzt man in (4.7) das CO2-Trägheitsmoment ICO2 aus (4.3) ein, so erhält man für die CO2-Rotationskonstante:

$$B_{fCO_2 } = \frac{h}{{8 \cdot \pi ^2 \cdot I_{CO_2 } }} = \frac{{6,6261 \cdot 10^{ - 34} Js}}{{8 \cdot \pi ^2 \cdot 7,0278 \cdot 10^{ - 46} Js^2 }} = 11,94GHz$$

(4.8)

Als nächstes soll berechnet werden, welche Energie notwendig ist, um die Rotation von einem Zustand J auf den folgenden Zustand J+1 zu erhöhen. Dazu müssen die Rotationsenergien zweier aufeinander folgender Zustände voneinander subtrahiert werden:

$$E_{J + 1} - E_J = B_f \cdot h \cdot \left( {J + 1} \right) \cdot \left( {J + 2} \right) - B_f \cdot h \cdot J \cdot \left( {J + 1} \right) = B_f \cdot h \cdot \left( {J + 1} \right) \cdot \left( {J + 2 - J} \right)$$

$$E_{J + 1} - E_J = 2 \cdot B_f \cdot h \cdot \left( {J + 1} \right)$$

(4.9)

Die Abstände zwischen zwei aufeinander folgenden Energieniveaus EJ und EJ+1 nehmen also nach (4.9) mit J zu. Das bedeutet, es muss mit jedem Übergang auf ein höheres Rotationsniveau mehr Energie aufgewendet werden, als beim vorherigen Übergang. Das führt auch dazu, dass die Moleküle nicht endlos schnell drehen können, sondern nur so schnell, wie sie von den sich am schnellsten um sie herum bewegenden Teilchen angestoßen werden können. In Tabelle 4-1 sind die jeweiligen Übergänge mit den dazu nötigen Energien nach (4.9) eingetragen.

Aus Tabelle 4-1 ist aber sofort ersichtlich, dass sich der für einen Rotationsübergang notwendige Energiebedarf mit jedem Schritt um 2·Bf·h erhöht. Gesetzt den Fall, man kann diese Energie mittels elektromagnetischer Strahlung zuführen, dann muss das anregende Lichtteilchen (Photon) eine sich nach (4.9) zu berechnende Energie besitzen.

$$B_f \cdot \left( {J + 1} \right) \cdot h = f_{J \to J + 1} \cdot h$$

(4.10)

Dabei ist fJ→J+1 die Frequenz der zur Rotation anregenden elektromagnetischen Strahlung und h das schon benannte Plancksche Wirkungsquantum. Für eine Rotationsanregung ist also ein Frequenzspektrum mit einem Frequenzabstand von 2·Bf nötig.

$$\Delta f = 2 \cdot B_f $$

(4.11)

Damit die Rotation eines Moleküls mittels elektromagnetischer Strahlung angeregt werden kann, muss es ein permanentes Dipolmoment besitzen. Das bedeutet, es muss verteilte Ladungsschwerpunkte besitzen. Alle so genannten homonuklearen zweiatomigen Moleküle, wie z.B. die hauptsächlichen Atmosphärenbestandteile N2 und O2, besitzen kein Dipolmoment und können somit auch nicht mit elektromagnetischer Strahlung in Wechselwirkung treten. Das gleiche gilt auch für CO2, bei dem es durch seinen symmetrischen Aufbau auch nicht zu einer Ausbildung von Ladungsschwerpunkten kommt.

   
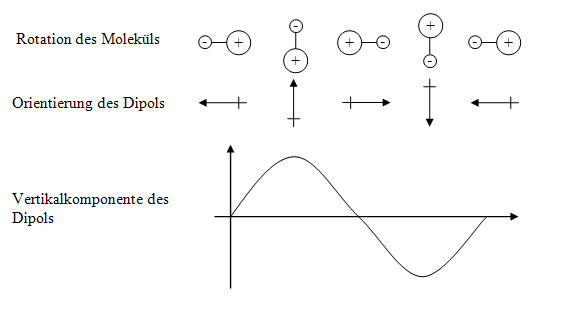
   Abb. 4-3: Rotation eines Moleküls mit Dipolmoment, z.B. HCl

In Abbildung 4-3 ist die Rotation eines zweiatomigen Moleküls mit Dipolcharakter dargestellt. Als Beispiel wird in der Literatur oft das Salzsäuremolekül HCl genannt. Wenn ein ortsfester Beobachter dieses Teilchen rotieren sehen könnte, so würde es für ihn ein veränderliches Dipolmoment besitzen, an dem ein elektromagnetisches Feld angreifen kann. Man sagt auch, dass dieses Molekül hinsichtlich optischer Absorption aktiv ist. Wenn die Frequenz stimmt, kann dieses Molekül elektromagnetische Strahlung absorbieren (aufnehmen) und seine Rotationsgeschwindigkeit erhöhen. Genauso kann ein rotierendes HCl-Molekül ein Photon elektromagnetischer Strahlung unter Verringerung seiner Rotationsgeschwindigkeit emittieren (abgeben). Die Frequenzen sind, wie bereits geschildert, fest vom Molekülaufbau vorgeschrieben.

   
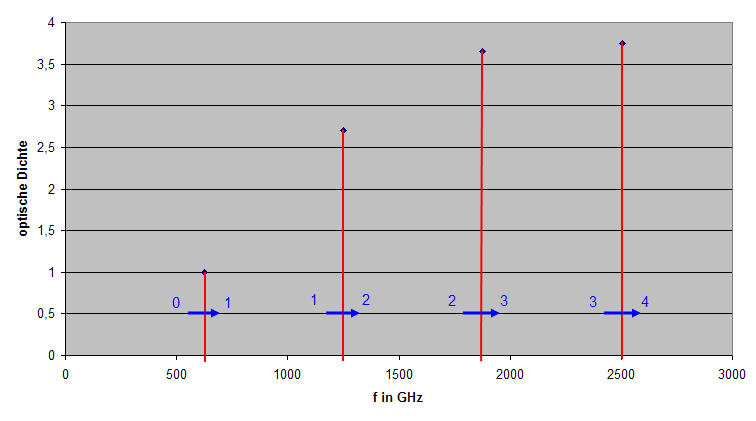
   Abb. 4-4: Mikrowellenspektrum von HCl

In Abbildung 4-4 ist der Anfang des Mikrowellenspektrums von HCl dargestellt. Die erste Linie beginnt bei 2·B=625,9GHz, was einen Übergang von J=0 nach J=1 bedeutet und die nächsten Linien setzen sich in diesem Abstand fort. Durch das Dipolmoment ist dieses Spektrum direkt messbar. Die homonuklearen zweiatomigen Hauptbestandteile der Luft N2 und O2, sowie das symmetrische Spurengas CO2 strahlen nicht durch Rotation.

Trotzdem tritt bei diesen Molekülen thermisch angeregte Rotation auf. Wird durch Stöße von benachbarten Molekülen im richtigen Winkel genug kinetische Energie übertragen, setzt die Rotation ein, während das stoßende Teilchen diesen Betrag an Energie an seiner Geschwindigkeit verliert. Die Rotation wirkt wie ein zusätzlicher Energiespeicher und erhöht somit die die Wärmekapazität des Gases.

Wie man sich leicht vorstellen kann, hängt der Grad der Rotation von der Temperatur ab. Je höher die Temperatur ist, umso mehr Teilchen haben die nötige Energie, um einen höheren Zustand J der Rotation anzuregen. Im statistischen Mittel sind die einzelnen Zustände in Abhängigkeit von der Temperatur nach der so genannten Boltzmann-Verteilung verteilt. Die Boltzmann-Verteilung für diskrete Zustände lautet allgemein:

$$N_J = N_0 \cdot g_J \cdot e^{ - \frac{{E_J }}{{k_B \cdot T}}} $$

(4.12)

Hierbei bezeichnet NJ die Anzahl der Teilchen, die den Zustand J besetzen, N0 die Teilchenzahl des 0-ten Zustands, gJ den so genannten Entartungsgrad des Zustands J und kB = 1,380658·10^-23J/K die Boltzmann-Konstante. Der Entartungsgrad bezeichnet die Anzahl von Zuständen gleicher Energie EJ. Für die Rotation linearer Moleküle wird der Entartungsgrad nach dem Buch "Molekülphysik und Quantenchemie" (Haken/Wolf, Springer-Verlag, Heidelberg, 1991, S.141) angegeben mit:

$$g_J = 2 \cdot J + 1$$

(4.13)

Die Verteilungsformel für die Rotation ergibt sich dann aus (4.5), (4.12) und (4.13):

$$N_J = N_0 \cdot \left( {2 \cdot J + 1} \right) \cdot e^{ - \frac{{B_f \cdot h \cdot J \cdot \left( {J + 1} \right)}}{{k_B \cdot T}}} $$

(4.14)

Abbildung 4-5 zeigt die Boltzmann-Statistik der Rotation von CO2 bei einer mittleren Erdtemperatur von +15°C, wobei der Einfachheit halber N0=1 gesetzt wurde. Die Höhe der Linien ist proportional zur Anzahl der Moleküle mit gleicher Rotationsgeschwindigkeit. Sie entspräche auch der Linienintensität im Rotationsspektrum bei Molekülen mit Dipolcharakter.

   
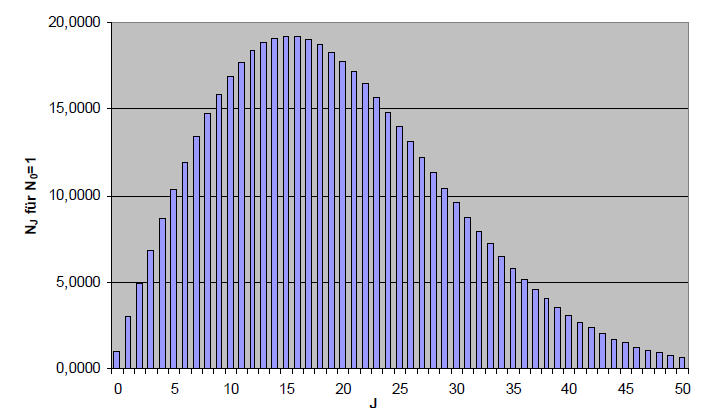
   Abb. 4-5: Boltzmann-Verteilung der Rotation von CO2 bei +15°C

Das ist auch leicht einzusehen, da bei vielen Molekülen die Wahrscheinlichkeit steigt, dass die Energie eines Photons in Erhöhung der Drehgeschwindigkeit umgesetzt werden kann. Für kleine J wächst nach (4.14) die Linienintensität und für größere J überwiegt die Abnahme der Exponentialfunktion. Dazwischen liegt ein Intensitätsmaximum.