7. Linienbreiten

Die natürliche Linienbreite ist die immer vorhandene minimale Linienbreite, die durch die begrenzte Lebensdauer τ des angeregten Zustandes hervorgerufen wird. So wie jede elektromagnetische Strahlungsquelle durch Abstrahlung Energie verliert, entvölkert sich ein angeregter Molekülzustand. Die Anzahl der Moleküle in einem angeregten Zustand nimmt im Laufe der Zeit durch Abgabe von Photonen exponentiell ab. Analog zum radioaktiven Zerfall kann für diesen Prozess eine Halbwertszeit T½ angeben werden. Die Abklingrate der Schwingung kann man mit folgender Exponentialfunktion beschreiben:

$$N(t) = N_0 \cdot \left( {\frac{1}{2}} \right)^{\frac{t}{{T_{1/2} }}} = N_0 \cdot 2^{ - \frac{t}{{T_{1/2} }}} $$

(7.1)

Dabei ist N0 die Anzahl der Moleküle im angeregten Zustand zum Zeitpunkt t = 0. Entsprechend ist N(t) die Anzahl der angeregten Moleküle zum Zeitpunkt t. Als nächstes wird (7.1) in die Logarithmusfunktion zur Basis 2 überführt:

$$ld\left( {\frac{{N(t)}}{{N_0 }}} \right) = - \frac{t}{{T_{1/2} }}$$

(7.2)

Nach den Logarithmusgesetzen kann der Logarithmus zur Basis 2 in den natürlichen Logarithmus zur Basis e überführt werden. Aus (7.2) wird somit:

$$ld\left( {\frac{{N(t)}}{{N_0 }}} \right) = \frac{{\ln \left( {\frac{{N(t)}}{{N_0 }}} \right)}}{{\ln 2}} = - \frac{t}{{T_{1/2} }}$$

→

$$\ln \left( {\frac{{N(t)}}{{N_0 }}} \right) = - \frac{t}{{\frac{{T_{1/2} }}{{\ln 2}}}} = - \frac{t}{\tau }$$

(7.3)

Der Ausdruck τ = T½/ln2 wird als mittlere Lebensdauer des angeregten Zustands bezeichnet. In Exponentialschreibweise wird aus (7.3):

$$N(t) = N_0 \cdot e^{ - \frac{t}{\tau }} $$

(7.4)

Die Strahlungsintensität I(t) verhält sich direkt proportional zur Anzahl N(t) der angeregten Moleküle und nimmt deshalb ebenfalls exponentiell ab. Es gilt folgende Beziehung:

$$I(t) = I_0 \cdot e^{ - \frac{t}{\tau }} $$

(7.5)

Die Intensität wird in der Einheit W/m² gemessen, sie ist also die auf ein Flächenelement eingestrahlte Leistung. Die Leistung verhält sich aber analog zur potentiellen Energie gemäß (5.12) quadratisch zum Abstand der Atomkerne und damit quadratisch zur Amplitude der Schwingung. Das Molekül kann man sich auch als einen geladenen Kondensator vorstellen, dessen Plattenabstand im Rhythmus der Schwingung geändert wird. Dadurch entsteht ein sich änderndes elektrisches Feld. Die Bewegung von Ladungsträgern bewirkt aber nach dem Induktionsgesetz ein magnetisches Feld. Das schwingende Molekül kann man sich also auch als einen Elementarschwingkreis vorstellen. Eine Schwingung kann man, wie bereits beschrieben, komplex mit der Eulerschen Formel darstellen. So ergibt sich nach (7.5) für das sich ändernde magnetische bzw. elektrische Feld A(t) die Gleichung einer gedämpften Schwingung:

$$A(t) = A_0 \cdot \sqrt {e^{ - \frac{t}{\tau }} } \cdot e^{j \cdot \omega _0 \cdot t} = A_0 \cdot e^{ - \frac{t}{{2 \cdot \tau }}} \cdot e^{j \cdot \omega _0 \cdot t} $$

(7.6)

Dabei ist ω0 = 2·π·f0 die Kreisfrequenz der ungedämpften Schwingung und A0 ihre Amplitude. Die Wurzel wurde entsprechend den Potenzgesetzen zu einer Division im Exponenten aufgelöst. Die Gleichung (7.6) kann so interpretiert werden, dass zum Zeitpunkt t=0 alle Moleküle des Systems gleichzeitig durch einen Impuls zum Schwingen angeregt werden. Alle Schwingungen ergeben zum Zeitpunkt t=0 gemeinsam die Amplitude A0. Durch die Abstrahlung von Photonen entvölkert sich der angeregte Zustand exponentiell – die Elementarschwingkreise fallen aus – und die Amplitude A(t) als Summe der Einzelamplituden wird entsprechend gedämpft.

Um zu sehen, wie sich dieses Verhalten im Frequenzbereich widerspiegelt, wird (7.6) einer Fouriertransformation unterzogen:

$$\hat A(\omega ) = \int\limits_0^\infty {A_0 \cdot e^{ - \frac{t}{{2 \cdot \tau }}} \cdot e^{j \cdot \omega _0 \cdot t} \cdot e^{ - j \cdot \omega \cdot t} dt} = A_0 \cdot \int\limits_0^\infty {e^{ - \left( {\frac{1}{{2 \cdot \tau }} + j \cdot \left( {\omega - \omega _0 } \right)} \right) \cdot t} dt} $$

$$\hat A(\omega ) = - \frac{{A_0 }}{{\frac{1}{{2 \cdot \tau }} + j \cdot \left( {\omega - \omega _0 } \right)}} \cdot \left[ {e^{ - \left( {\frac{1}{{2 \cdot \tau }} + j \cdot \left( {\omega - \omega _0 } \right)} \right) \cdot t} } \right]_0^\infty = \frac{{A_0 }}{{\frac{1}{{2 \cdot \tau }} + j(\omega - \omega _0 )}}$$

(7.7)

Um von der komplexen Darstellung zu einer reellen Darstellung zu kommen, wird (7.7) konjugiert komplex erweitert. Somit erhält man das reelle Betragsquadrat der Amplitude.

$$\left| {\hat A(\omega )} \right|^2 = \frac{{A_0 }}{{\frac{1}{{2 \cdot \tau }} + j(\omega - \omega _0 )}} \cdot \frac{{A_0 }}{{\frac{1}{{2 \cdot \tau }} - j(\omega - \omega _0 )}} = \frac{{A_0^2 }}{{\left( {\omega - \omega _0 } \right)^2 + \left( {\frac{1}{{2 \cdot \tau }}} \right)^2 }}$$

(7.8)

Analog (7.5) und (7.6) ist die Intensität proportional zum Quadrat der Amplitude, so dass man aus (7.8) folgern kann:

$$\frac{{\hat I(\omega )}}{{\hat I_0 }} \propto \frac{1}{{\left( {\omega - \omega _0 } \right)^2 + \left( {\frac{1}{{2 \cdot \tau }}} \right)^2 }}$$

(7.9)

Der rechte Ausdruck muss aber für ω = ω0 den Wert 1 ergeben, damit gelten kann:

$$\hat I(\omega = \omega _0 ) = \hat I_0 $$

Somit wird aus (7.9) die Gleichung:

$$\hat I(\omega ) = \hat I_0 \cdot \frac{{\left( {\frac{1}{{2 \cdot \tau }}} \right)^2 }}{{\left( {\omega - \omega _0 } \right)^2 + \left( {\frac{1}{{2 \cdot \tau }}} \right)^2 }}$$

(7.10)

Die Spektrallinie erhält damit genau wie ein Schwingkreis die Form einer Lorentzkurve. Viele Elementaroszillatoren geben somit Photonen einer Frequenz ab, die sich in ihrer Intensität nach (7.10) verteilen. Die Kurvenform von (7.10) ist in Abbildung 7-1 dargestellt.

   
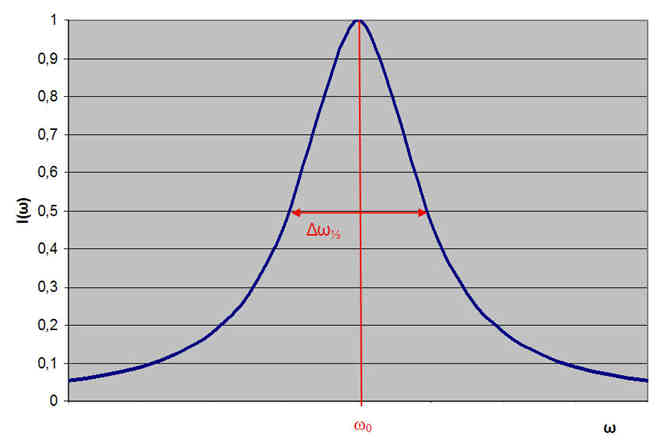
   Abb. 7-1: Linienform einer Spektrallinie mit Lorentzprofil

Neben der Höhe der Kurve bei I0 ist die so genannte Halbwertsbreite entscheidend. Unter der Halbwertsbreite einer Spektrallinie Δω½ versteht man ihre Breite auf der halben Höhe ihres Spitzenwertes. Für ein Lorentz-Profil ist diese gleich dem Parameter 1/τ. Man kann also schreiben:

$$\Delta \omega _{1/2} = \frac{1}{\tau }$$

(7.11)

Wenn man die Spektrallinie wie bereits angedeutet mit einem Schwingkreis vergleicht, so entspricht Δω½ genau seiner Bandbreite. Bei Darstellung des Stroms in Abhängigkeit von der Frequenz ist die Bandbreite des Schwingkreises definiert als der Frequenzbereich, an dessen Grenzen sich der Strompegel um den Faktor 1/√2 = 0,707 als linearer Faktor gegenüber dem Extremwert geändert hat. Da (7.10) aber eine Intensität bzw. Leistung beschreibt, muss dieses Verhältnis quadriert werden, so dass für eine gegebene Bandbreite die Intensität um den Faktor ½ sinken muss. Eng mit der Bandbreite verbunden ist der Dämpfungsfaktor d. Er ist definiert als das Verhältnis der Bandbreite zur Resonanzfrequenz. Es gilt also:

$$d = \frac{{\Delta \omega _{1/2} }}{{\omega _0 }} = \frac{{\Delta f_{1/2} }}{{f_0 }} = \frac{1}{{\tau \cdot \omega _0 }}$$

(7.12)

In der Diplomarbeit "Umbau und Test der Heidelberger Methan-Isotopen-Aufbereitung für die δD-Analyse von Reinluftproben mit Infrarotabsorptionsspektroskopie" (Cordelia Veidt, Ruprecht-Karls-Universität Heidelberg Studiengang Physik, März 2002, S. 47) wird die natürliche Linienbreite (= Halbwertsbreite) von Absorptionslinien für Rotations-Vibrations-Übergänge in der Größenordnung von 10^-8cm^-1 angegeben. Analog (4.6) entspricht dieser Wert einer Frequenz von (c = Lichtgeschwindigkeit):

$$\Delta f_{1/2} = c \cdot 10^{ - 8} cm^{ - 1} = \frac{{3 \cdot 10^8 \frac{m}{s}}}{{10^6 m}} = 300Hz$$

(7.13)

Der Dämpfungsfaktor durch Abstrahlung ist wegen der niedrigen Bandbreite nach (7.13) und der hohen Resonanzfrequenz v2 nach Tabelle 5-1 sehr niedrig und berechnet sich zu:

$$d = \frac{{\Delta f_{1/2} }}{{f_0 }} = \frac{{300Hz}}{{20,01THz}} = 1,5 \cdot 10^{ - 11} $$

(7.14)