7. Linienbreiten

Die Dopplerverbreiterung einer Spektrallinie entsteht durch den Dopplereffekt der ungeordneten thermischen Bewegung der Moleküle. Bewegt sich ein Molekül mit der Geschwindigkeit vx in Richtung auf den Beobachter zu und emittiert dabei Strahlung der Frequenz f0, so erreicht ihn diese infolge des relativistischen Dopplereffektes mit der Frequenz f:

$$f = f_0 \cdot \sqrt {\frac{{c + v_x }}{{c - v_x }}} $$

(7.15)

Bewegt sich das emittierende Molekül dagegen mit vx vom Beobachter weg, so verringert sich die empfangene Frequenz zu:

$$f = f_0 \cdot \sqrt {\frac{{c - v_x }}{{c + v_x }}} $$

(7.16)

Dabei ist c die Lichtgeschwindigkeit von ca. 300000000m/s. Für die Frequenzverschiebung Δf für ein entgegenkommendes Molekül ergibt sich nach (7.15):

$$\Delta f = f - f_0 = f_0 \cdot \sqrt {\frac{{c + v_x }}{{c - v_x }}} - f_0 = f_0 \cdot \left( {\sqrt {\frac{{c + v_x }}{{c - v_x }}} - 1} \right)$$

(7.17)

Der Wurzelausdruck wird in eine Potenzreihe entwickelt. Als Ausgangspunkt wird folgende binomische Reihe verwendet (Lothar Papula, "Mathematische Formelsammlung für Ingenieure und Naturwissenschaftler", Vieweg & Sohn Verlagsgesellschaft mbH, Braunschweig, 3.Auflage, 1990, S.156):

$$\sqrt {1 - x} = 1 - \frac{1}{2} \cdot x - \frac{1}{2} \cdot \frac{1}{4} \cdot x^2 - \frac{1}{2} \cdot \frac{1}{4} \cdot \frac{3}{6} \cdot x^3 - \frac{1}{2} \cdot \frac{1}{4} \cdot \frac{3}{6} \cdot \frac{5}{8} \cdot x^4 - ...$$

(7.18)

Da vx sehr viel kleiner als die Lichtgeschwindigkeit ist, genügt die Verwendung des ersten Gliedes von (7.18). Um (7.18) nutzen zu können, wird der Wurzelausdruck von (7.17) auf die Form 1-x gebracht:

$$1 - x = \frac{{c + v_x }}{{c - v_x }}$$

→

$$x = 1 - \frac{{c + v_x }}{{c - v_x }}$$

(7.19)

Somit lässt sich der Wurzelausdruck aus (7.17) mit Hilfe von (7.18) und (7.19) vereinfachen:

$$\sqrt {\frac{{c + v_x }}{{c - v_x }}} - 1 = \sqrt {1 - \left( {1 - \frac{{c + v_x }}{{c - v_x }}} \right)} - 1 \approx 1 - \frac{1}{2} \cdot \left( {1 - \frac{{c + v_x }}{{c - v_x }}} \right) - 1 \approx \frac{1}{2} \cdot \left( {\frac{{c + v_x }}{{c - v_x }} - \frac{{c - v_x }}{{c - v_x }}} \right) \approx \frac{{v_x }}{{c - v_x }} \approx \frac{{v_x }}{c}$$

(7.20)

Es ergibt sich für kleine vx aus (7.17) und (7.18) folgende einfache Beziehung für Δf:

$$\Delta f \approx f_0 \cdot \frac{{v_x }}{c}$$

(7.21)

Die Geschwindigkeitsverteilung der Moleküle in Beobachtungsrichtung ist durch eine Maxwell-Boltzmann-Verteilung gegeben, wobei vx wieder klein gegen die Lichtgeschwindigkeit c ist:

$$\frac{{dN}}{{dv_x }} = N_0 \cdot \sqrt {\frac{m}{{2 \cdot \pi \cdot k_B \cdot T}}} \cdot e^{ - \frac{{m \cdot \nu _x^2 }}{{2 \cdot k_B \cdot T}}} $$

(7.22)

Dabei ist N0 die Gesamtzahl der Moleküle, m die Masse eines Moleküls, kB die Boltzmann-Konstante und T die absolute Temperatur. Um zu einer Frequenzverteilung zu kommen, wird (7.21) nach vx umgestellt und in (7.22) eingesetzt:

$$\frac{{dN}}{{dv_x }} = N_0 \cdot \sqrt {\frac{m}{{2 \cdot \pi \cdot k_B \cdot T}}} \cdot e^{ - \frac{{m \cdot \nu _x^2 }}{{2 \cdot k_B \cdot T}}} $$

(7.23)

Nun wird in (7.23) dvx durch df substituiert, indem vx nach f abgeleitet wird:

$$v_x = c \cdot \frac{{f - f_0 }}{{f_0 }}$$

→

$$\frac{{dv_x }}{{df}} = \frac{c}{{f_0 }}$$

→

$$dv_x = \frac{c}{{f_0 }} \cdot df$$

$$\frac{{dN}}{{df}} = N_0 \cdot \frac{c}{{f_0 }} \cdot \sqrt {\frac{m}{{2 \cdot \pi \cdot k_B \cdot T}}} \cdot e^{ - \frac{{m \cdot c^2 }}{{2 \cdot k_B \cdot T}} \cdot \frac{{\left( {f - f_0 } \right)^2 }}{{f_0^2 }}} = N_0 \cdot \sqrt {\frac{{m \cdot c^2 }}{{2 \cdot \pi \cdot k_B \cdot T \cdot f_0^2 }}} \cdot e^{ - \frac{{m \cdot c^2 }}{{2 \cdot k_B \cdot T}} \cdot \frac{{\left( {f - f_0 } \right)^2 }}{{f_0^2 }}} $$

(7.24)

Die Gleichung (7.24) ist aber die Gaußsche Normalverteilung mit dem Mittelwert μ=f0 und der Standardabweichung σ.

$$\frac{{dN}}{{N_0 \cdot df}} = \frac{1}{{\sqrt {2 \cdot \pi } \cdot \sigma }} \cdot e^{ - \frac{1}{2} \cdot \left( {\frac{{f - f_0 }}{\sigma }} \right)^2 } $$

mit

$$\sigma = \frac{{m \cdot c^2 }}{{k_B \cdot T \cdot f_0^2 }}$$

(7.25)

Da sich die Intensität proportional zur Anzahl der strahlenden Moleküle verhält, ergibt sich, dass auch das Dopplerverbreiterte Profil einer (streng monochromatischen) Linie eine Gaußsche Kurve ist. Mit Î0 als Intensitätsmaximum der Kurve bei f=f0 lässt sich somit aus (7.25) ableiten:

$$\hat I(f) = \hat I_0 \cdot e^{ - \frac{{m \cdot c^2 }}{{2 \cdot k_B \cdot T}} \cdot \frac{{\left( {f - f_0 } \right)^2 }}{{f_0^2 }}} $$

(7.26)

Î(f) ist die Intensität einer Spektrallinie bestimmter Frequenz. Die Halbwertsbreite Δf½ einer solchen Linie beträgt:

$$\frac{{\hat I\left( {f_{1/2} } \right)}}{{\hat I_0 }} = \frac{1}{2} = e^{ - \frac{{m \cdot c^2 }}{{2 \cdot k_B \cdot T}} \cdot \frac{{\left( {f_{1/2} - f_0 } \right)^2 }}{{f_0^2 }}} $$

→

$$\ln \left( {\frac{1}{2}} \right) = - \ln \left( 2 \right) = - \frac{{m \cdot c^2 }}{{2 \cdot k_B \cdot T}} \cdot \frac{{\left( {f_{1/2} - f_0 } \right)^2 }}{{f_0^2 }}$$

$$\ln \left( 2 \right) \cdot \frac{{2 \cdot k_B \cdot T}}{{m \cdot c^2 }} = \frac{{\left( {f_{1/2} - f_0 } \right)^2 }}{{f_0^2 }}$$

→

$$f_{1/2} = f_0 \pm \sqrt {\ln \left( 2 \right) \cdot \frac{{2 \cdot k_B \cdot T \cdot f_0^2 }}{{m \cdot c^2 }}} $$

$$\Delta f_{1/2} = 2 \cdot f_0 \cdot \sqrt {2 \cdot \ln \left( 2 \right) \cdot \frac{{k_B \cdot T}}{{m \cdot c^2 }}} $$

(7.27)

Aus (7.27) kann man sehen, dass die Verbreiterung der Linie nur von der Temperatur abhängt und nicht vom Druck. Für eine Temperatur von +15°C ergibt sich für CO2 folgende Dopplerbreite:

$$\Delta f_{1/2} = 2 \cdot 20THz \cdot \sqrt {2 \cdot \ln \left( 2 \right) \cdot \frac{{1,38 \cdot 10^{ - 23} \frac{J}{K} \cdot 288K}}{{44 \cdot 1,66 \cdot 10^{ - 27} kg \cdot 9 \cdot 10^{16} \frac{{m^2 }}{{s^2 }}}}} = 36,62MHz$$

(7.28)

Ein Vergleich von (7.28) mit (7.13) zeigt, dass die natürliche Linienbreite gegenüber der Dopplerbreite verschwindend gering ist und somit vernachlässigt werden kann.

   
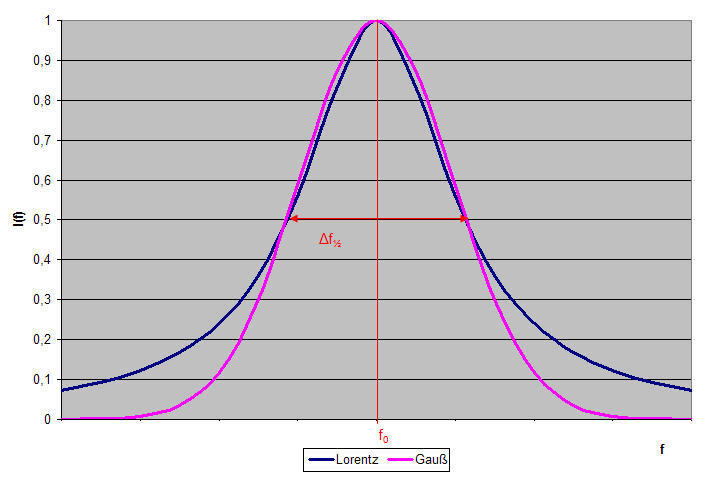
   Abb. 7-2: Vergleich Lorentzprofil mit Gaußprofil

Die natürliche Linienbreite, bedingt durch die endliche Lebensdauer der angeregten Zustände, besitzt ein Lorentzprofil, während die Dopplerverbreiterung ein Gaußprofil aufweist. Der Vergleich in Abbildung 7-2 zeigt, dass das Lorentzprofil bei gleicher Höhe und Halbwertsbreite flachere Linienflügel hat.