9. Die Lücken im Spektrum

Ein Blick auf Abbildung 6-3 zeigt, dass sich zwischen den einzelnen Spektrallinien Lücken befinden. Der Abstand zwischen zwei Linien beträgt nach (6.3) 4·Bf = 46,15GHz. Nach Kapitel 7 besitzt jede Linie eine gewisse Breite, die nach Kapitel 8 mit wachsender Konzentration des Mediums bzw. mit wachsender Weglänge (und damit wachsender prozentualer Absorption) steigt. Die Frage ist nun, wann bzw. wo sich diese Lücken schließen.

Die Firma GORATEC Engineering GmbH ist Spezialist für Infrarotkameras und Infrarotsensoren. Auf ihrer Internetseite zum Thema Thermographie ist die Theorie der Infrarotaufnahmetechnik sehr ausführlich abgehandelt. Im Abschnitt "Einfluss der Atmosphäre" steht:

"… dass in bestimmten Wellenlängenbereichen (z.B. 2,6 bis 2,9μm; 4,3 bis 4,5μm; 5,4 bis 7,0μm) die Strahlung nahezu vollständig gedämpft, absorbiert wird. Den größten Anteil haben Kohlendioxid (CO2) und Wasserdampf (H20), die sich schon bei kürzesten Entfernungen bemerkbar machen. Die Streuungseffekte werden hauptsächlich durch in der Luft schwebende Teilchen wie z.B. Staub und Wassertropfen verursacht. Im langwelligen Bereich 8μm bis 13μm werden die Verhältnisse günstiger. Die wellenlängenabhängige Dämpfung der Strahlung ist durch den spektralen Transmissionsgrad definiert, welcher sich aus dem Produkt einzelner Transmissionsgrade der Moleküle ergibt."

   
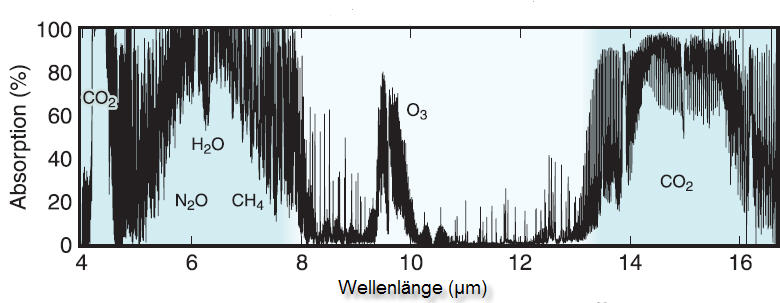
   Abb. 9-1: Absorption der Erdatmosphäre durch infrarotaktive Moleküle, (Quelle: IPCC, Special Report on Safeguarding the Ozone and the Global Climate System, S.156)

In Abbildung 9-1 ist die Absorption der Erdatmosphäre durch verschiedene infrarotaktive Moleküle dargestellt. Auffällig ist die Totalabsorption von CO2 im 15μm-Bereich. Die Industrie hat offensichtlich die Erfahrung gemacht, dass Infrarotsensoren für Bereiche ausgelegt sein müssen, in denen das atmosphärische Fenster offen ist und nicht durch infrarotaktive Gase beeinflusst wird (nämlich 3-5μm und 8-13μm). In den Bereichen, wo CO2 und H2O aktiv sind, herrscht sozusagen schon nach kurzer Distanz völlige Blindheit. Es ist also davon auszugehen, dass die einzelnen Rotationsschwingungslinien ineinander übergehen, so dass innerhalb des Bandenspektrums die Energie vollständig absorbiert wird und nicht ein Teil durch die Lücken zwischen den Spektrallinien entweichen kann.

Aus (6.3) wissen wir den Abstand zwischen zwei Linien und aus (7.45) kennen wir den Fremdverbreiterungskoeffizienten von CO2 in Luft unter Normalbedingungen (1013hPa und +23°C). Zunächst soll nach (7.41) für normalen Luftdruck der Fremdverbreiterungskoeffizient für +15°C Erdmitteltemperatur bestimmt werden:

$$\Delta f_{1/2} = \Delta f_{1/2fremd}^0 \cdot \left( {\frac{{T_0 }}{T}} \right)^{0,7} = 4,482GHz \cdot \left( {\frac{{296K}}{{288K}}} \right)^{0,7} = 4,569GHz$$

(9.1)

Als nächstes wird (7.29) so umgeformt, dass der Fremdverbreiterungskoeffizient (bzw. die Halbwertsbreite) direkt eingesetzt werden kann. Dazu wird die Kreisfrequenz aufgelöst:

$$\frac{{\hat I(f)}}{{\hat I_0 }} = \frac{{4 \cdot \pi ^2 \cdot \left( {\frac{1}{{4 \cdot \pi \cdot \tau _S }}} \right)^2 }}{{4 \cdot \pi ^2 \cdot \left( {f - f_0 } \right)^2 + 4 \cdot \pi ^2 \cdot \left( {\frac{1}{{4 \cdot \pi \cdot \tau _S }}} \right)^2 }} = \frac{{\left( {\frac{1}{{4 \cdot \pi \cdot \tau _S }}} \right)^2 }}{{\left( {f - f_0 } \right)^2 + \left( {\frac{1}{{4 \cdot \pi \cdot \tau _S }}} \right)^2 }}$$

Und nun wird nach (7.11) die Zeitkonstante τS durch die Halbwertsbreite substituiert:

$$\frac{{\hat I(f)}}{{\hat I_0 }} = \frac{{\left( {\frac{{\Delta f_{1/2} }}{2}} \right)^2 }}{{\left( {f - f_0 } \right)^2 + \left( {\frac{{\Delta f_{1/2} }}{2}} \right)^2 }}$$

(9.2)

Wenn zwei Linien einen Abstand von 4·B besitzen, müssen sie sich im Abstand von f–f0 = 2·Bf schneiden. Damit ergibt sich aus (9.2) das Intensitätsverhältnis:

$$\frac{{\hat I_{2 \cdot B_f } }}{{\hat I_0 }} = \frac{{\left( {\frac{{\Delta f_{1/2} }}{2}} \right)^2 }}{{\left( {2 \cdot B_f } \right)^2 + \left( {\frac{{\Delta f_{1/2} }}{2}} \right)^2 }} = \frac{{\left( {\Delta f_{1/2} } \right)^2 }}{{\left( {4 \cdot B_f } \right)^2 + \left( {\Delta f_{1/2} } \right)^2 }} = \frac{{\left( {4,569GHz} \right)^2 }}{{\left( {46,15GHz} \right)^2 + \left( {4,569GHz} \right)^2 }} = 0,00971$$

(9.3)

Damit ist im Schnittpunkt zweier benachbarter Linien die Intensität auf ca. 1% des Linienmaximums zurückgegangen. Da die benachbarte Linie in etwa gleich groß ist, muss die Intensität im Schnittpunkt in erster Näherung verdoppelt werden, so dass wir etwa 2% des Maximums annehmen können.

Nach (8.18) kann unter Berücksichtigung von (7.11) das Intensitätsverhältnis auch über die Formfunktion ausgedrückt werden:

$$\frac{{\hat I_{2 \cdot B_f } }}{{\hat I_0 }} = \frac{1}{{4 \cdot \tau _S }} \cdot g_{2 \cdot B_f } = \frac{{2 \cdot \pi \cdot \Delta f_{1/2} }}{4} \cdot g_{2 \cdot B_f } = \frac{\pi }{2} \cdot \Delta f_{1/2} \cdot g_{2 \cdot B_f } $$

→

$$g_{2 \cdot B_f } = \frac{{\hat I_{2 \cdot B_f } }}{{\hat I_0 }} \cdot \frac{2}{{\pi \cdot \Delta f_{1/2} }}$$

(9.4)

Nach (8.27) ist das aber gerade:

$$g_{2 \cdot B_f } = \frac{{\hat I_{2 \cdot B_f } }}{{\hat I_0 }} \cdot g(f_0 ) = 0,01 \cdot g(f_0 )$$

(9.5)

Wenn man nun (9.5) in das Lambert-Beersche-Gesetz in der Form nach (8.20) einsetzt, so erhält man die Absorption im Linienschnittpunkt.

$$A_{2 \cdot B_f } = 1 - e^{ - S \cdot 0,01 \cdot g\left( {f_0 } \right) \cdot c \cdot l} $$

(9.6)

Wenn man den Einfluss der benachbarten Linie bedenkt, so ist der Weg des durchstrahlten Mediums l bei gleicher Konzentration am Linienschnittpunkt etwa Fünfzig mal so lang zu wählen, um die gleiche Absorption wie im Linienmaximum zu erreichen.

Je mehr sich die prozentuale Absorption den 100% nähert, umso mehr verbreitert sich die Spektrallinie. Man kann sich nun eine prozentuale Absorption im Linienmaximum denken, bei der die Halbwertsbreite Δf½' bei 4·Bf liegt. Da hier auch in etwa die Halbwertsbreite der benachbarten Linie liegen muss, kommt es durchdie Addition der Linien zu einer Kurve ohne Wellen, die das gesamte Spektrum umfasst. Zur Berechnung gehen wir von (8.30) aus, wobei die Absorption A0 durch die Transmission T0 ersetzt wird (T0 = 1-A0):

$$\Delta f_{1/2}^/ = \Delta f_{1/2} \cdot \sqrt {\frac{{\ln \left( {T_0 } \right)}}{{\ln \left( {\frac{{2 - A_0 }}{2}} \right)}} - 1} = \Delta f_{1/2} \cdot \sqrt {\frac{{\ln \left( {T_0 } \right)}}{{\ln \left( {\frac{{1 + \left( {1 - A_0 } \right)}}{2}} \right)}} - 1} = \Delta f_{1/2} \cdot \sqrt {\frac{{\ln \left( {T_0 } \right)}}{{\ln \left( {\frac{{1 + T_0 }}{2}} \right)}} - 1} $$

(9.7)

Für Δf½' wird analog (9.3) der Wert von 46,15GHz eingesetzt und für Δf½ entsprechend der Wert von 4,569GHz. Dann wird noch etwas umgeformt:

$$\frac{{\Delta f_{1/2}^/ }}{{\Delta f_{1/2} }} = \frac{{46,15GHz}}{{4,569GHz}} = 10,1 = \sqrt {\frac{{\ln \left( {T_0 } \right)}}{{\ln \left( {\frac{{1 + T_0 }}{2}} \right)}} - 1} $$

→

$$103 = \frac{{\ln \left( {T_0 } \right)}}{{\ln \left( {\frac{{1 + T_0 }}{2}} \right)}}$$

$$103 \cdot \ln \left( {\frac{{1 + T_0 }}{2}} \right) = \ln \left( {T_0 } \right)$$

→

$$T_0 = e^{103 \cdot \ln \left( {\frac{{1 + T_0 }}{2}} \right)} = \left( {\frac{{1 + T_0 }}{2}} \right)^{103} $$

(9.8)

Die Gleichung (9.8) lässt sich nicht weiter nach T0 auflösen. Man kann aber (9.8) numerisch lösen, indem man T0 soweit nach 0 annähert, bis beide Seiten von (9.8) übereinstimmen. Das geschieht bei:

$$T_0 \approx 10^{ - 31} $$

(9.9)

Setzt man das Ergebnis nach (9.9) in das Lambert-Beersche-Gesetz nach (8.3) und (8.4) ein, so erhält man:

$$ - \ln \left( {T_0 } \right) = - \ln \left( {10^{ - 31} } \right) = 71,4 = \alpha _0 \cdot \int\limits_0^l {c\left( l \right) \cdot dl} $$

(9.10)

Um eine Aussage über α0 machen zu können, wird das von Dr. Heinz Hug gemessene CO2-Spektrum für die Deformationsschwingung bei 15μm (= 20THz) herangezogen. Das Spektrum wurde in dem Artikel "Die Klimakatastrophe – ein spektroskopisches Artefakt?" im Internet veröffentlicht und ist in Abbildung 9-2 dargestellt.

   
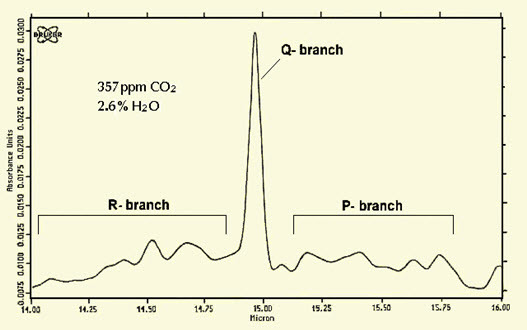
   Abb. 9-2: Spektrum der CO2-Deformationsschwingung bei 15μm, (Quelle: Dr. Heinz Hug, Die Klimakatastrophe – ein spektroskopisches Artefakt?)

Eine 10cm-Küvette mit IR-durchlässigem Fenster wurde mit synthetischer CO2- und H2O-freier Luft gefüllt. Danach wurde soviel CO2 mit einer Mikroliterspritze zugegeben, dass 357ppm CO2 zugegen waren (Konzentration von 1993). Weiter wurden 2,6 % Wasserdampf zugegeben. Als IR-Strahlungsquelle diente ein Globar, ein elektrisch auf 1000-1200 °C geheizter Siliziumkarbid-Stab mit nach geschaltetem variablen Interferenzfilter. Die Messung erfolgte mit einem FTIR-Spektrometer "Bruker IFS 48". Als Auswertungssoftware diente das Programm OPUS. Ein Nullwert wurde ebenfalls aufgenommen und entsprechend subtrahiert. Der Druck war normaler Luftdruck (1bar) und die Temperatur lag bei Raumtemperatur (+22°C).

Die relative Absorption im Maximum liegt bei 3%, so dass die Linienform der druckverbreiterten Linien nach Abbildung 8-3 noch unverzerrt dargestellt werden sollten. Die Auflösung ist aber schlecht, so dass die Linienform im R- und im P-Zweig nicht mehr gut erkennbar ist. Es wird für A0 ein Wert von 1% angenommen. Damit lässt sich nach (8.4) α0 folgendermaßen abschätzen:

$$ - \ln \left( {1 - A_0 } \right) = - \ln \left( {1 - 0,01} \right) = 0,01 = \alpha _0 \cdot c \cdot l = \alpha _0 \cdot c \cdot 0,1m$$

→

$$\alpha _0 = \frac{1}{{10m \cdot c}}$$

(9.11)

Die Konzentration c wird in der Spektroskopie üblicherweise in mol/m³ angegeben. Unter Normalbedingungen (0°C, 1bar) entspricht 1mol ein Volumen von 22,4l. Bei +22°C ist es entsprechend mehr. Man kann folgende Verhältnisgleichung aufstellen:

$$\frac{{22,4l}}{{273K}} = \frac{x}{{295K}}$$

→

$$x = 24,2l = 0,0242m^3 $$

Ein mol eines Gases nimmt also bei 22°C 0,0242m³ Rauminhalt ein. Andersherum kann man sagen, dass bei +22°C 1m³ Rauminhalt 41,3mol Teilchen enthält. Für eine Konzentration von 357ppm in der Atmosphäre gilt somit für das CO2:

$$c = \frac{{41,3mol}}{{m^3 }} \cdot 0,000357 = 0,0147\frac{{mol}}{{m^3 }}$$

(9.12)

Nun wird (9.12) in (9.11) eingesetzt und man erhält für α0:

$$\alpha _0 = \frac{1}{{10m \cdot c}} = \frac{1}{{10m \cdot 0,0147\frac{{mol}}{{m^3 }}}} = 6,8\frac{{m^2 }}{{mol}}$$

(9.13)

Analog (9.12) lässt sich auch die CO2-Konzentration bei +15°C durchschnittlicher Erdtemperatur und gegenwärtig 380ppm CO2 bei 1bar c0 bestimmen. Es gilt:

$$c_{15^\circ C/380ppm} = c_0 = \frac{{1mol}}{{\frac{{288K}}{{273K}} \cdot 0,0224m^3 }} \cdot 0,00038 = 0,0161\frac{{mol}}{{m^3 }}$$

(9.14)

Die CO2-Konzentration nach (9.14) gilt durchschnittlich auf Meereshöhe unter Normalbedingungen. Bei steigender Höhe h nehmen der Druck und damit auch die CO2-Konzentration ab. Für die Druckabnahme gilt nach dem Wikipedia-Artikel "Barometrische Höhenformel" die internationale Höhenformel bis zu einer Höhe von 11km:

$$p\left( h \right) = 1013,25hPa \cdot \left( {1 - \frac{{0,0065\frac{K}{m} \cdot h}}{{288,15K}}} \right)^{5,225} = 1013,25hPa \cdot \left( {1 - \frac{{0,00002256}}{m} \cdot h} \right)^{5,225} $$

(9.15)

Die Konzentration ist aber direkt proportional zum Druck, so dass nach (9.14) und (9.15) für den Konzentrationsverlauf analog gilt:

$$c\left( h \right) = c_0 \cdot \left( {1 - \frac{{0,00002256}}{m} \cdot h} \right)^{5,225} = 0,0161\frac{{mol}}{{m^3 }} \cdot \left( {1 - \frac{{0,00002256}}{m} \cdot h} \right)^{5,225} $$

(9.16)

Um jetzt die Höhe über dem Boden bestimmen zu können, bei der (9.9) erfüllt ist, werden (9.16) und (9.13) in (9.10) eingesetzt:

$$71,4 = 6,8\frac{{m^2 }}{{mol}} \cdot \int\limits_0^h {0,0161\frac{{mol}}{{m^3 }} \cdot \left( {1 - \frac{{0,00002256}}{m} \cdot h} \right)^{5,225} \cdot dh} $$

$$\int\limits_0^h {\left( {1 - \frac{{0,00002256}}{m} \cdot h} \right)^{5,225} \cdot dh = 652,2m} $$

(9.17)

Um das Integral von (9.17) lösen zu können, wird folgende Substitution durchgeführt:

$$x = 1 - \frac{{0,00002256}}{m} \cdot h$$

→

$$\frac{{dx}}{{dh}} = - \frac{{0,00002256}}{m}$$

→

$$dh = - 44326m \cdot dx$$

$$ - 44326m \cdot \int\limits_1^{1 - 0,00002256m^{ - 1} \cdot h} {x^{5,225} \cdot dx = 652,2m} $$

→

$$\int\limits_1^{1 - 0,00002256m^{ - 1} \cdot h} {x^{5,225} \cdot dx = - 0,0147} $$

Nun wird integriert:

$$\frac{1}{{6,225}} \cdot \left[ {x^{6,225} } \right]_1^{1 - 0,00002256m^{ - 1} \cdot h} = - 0,0147$$

→

$$\left[ {x^{6,225} } \right]_1^{1 - 0,00002256m^{ - 1} \cdot h} = - 0,0916$$

$$\left( {1 - 0,00002256m^{ - 1} \cdot h} \right)^{6,225} - 1 = - 0,0916$$

→

$$\left( {1 - 0,00002256m^{ - 1} \cdot h} \right)^{6,225} = 0,9084$$

Jetzt wird noch die Wurzel gezogen:

$$1 - 0,00002256m^{ - 1} \cdot h = \sqrt[{6,225}]{{0,9084}} = 0,9847$$

→

$$0,00002256m^{ - 1} \cdot h = 0,0153$$

→

$$h \approx 680m$$

(9.18)

Das bedeutet, dass bei ca. 700m über dem Boden die Transmission im 15μm-Band des CO2 nur noch bei ca. 10^-31 liegt. In dieser Höhe sind die einzelnen Rotationsschwingungslinien nicht mehr voneinander zu unterscheiden. Wegen der verschwindend geringen Transmission kann man im gesamten 15μm-Spektralbereich von einer Totalabsorption sprechen. Höher als 700m über den Boden kommt die in diesem Bereich von der Erde ausgestrahlte Infrarotstrahlung praktisch nicht.

Man kann auch für die untere Luftschicht den Absorptionskoeffizienten α0 und die Konzentration c0 zu einer Wegkonstanten λ0 folgendermaßen zusammenfassen:

$$\lambda _0 = \frac{1}{{\alpha _0 \cdot c_0 }} = \frac{1}{{6,8\frac{{m^2 }}{{mol}} \cdot 0,0161\frac{{mol}}{{m^3 }}}} = 9,13m$$

(9.19)

Das Lambert-Beersche-Gesetz lautet dann nach (8.2) und (9.19):

$$I\left( l \right) = I_0 \cdot e^{ - \frac{l}{{\lambda _0 }}} $$

(9.20)

Sobald l größer als λ0 wird, wird die Atmosphäre als optisch dicht bezeichnet, weil die Absorption schon bei 63% liegt. Bei einer Länge l = 3·λ0 liegt die Absorption bereits bei 95%, so dass man schon fast von Totalabsorption sprechen kann. Damit wird die meiste Infrarotstrahlungsenergie der Erde schon in den ersten knapp 30m über dem Erdboden absorbiert. Gemäß der Abbildung 9-1 ist das für den Treibhauseffekt wichtige Strahlungsfenster im 15μm-Bereich komplett geschlossen.