 |
"Deshalb müssen wir Schrecken einjagende Szenarien ankündigen, vereinfachende, dramatische Statements machen und wenig Erwähnung irgendwelcher Zweifel, die wir haben mögen, entlassen. Um Aufmerksamkeit zu erregen, brauchen wir dramatische Statements und keine Zweifel am Gesagten. Jeder von uns Forschern muss entscheiden, wie weit er eher ehrlich oder eher effektiv sein will."
Prof. Dr. Stephen Schneider, Chefautor der Arbeitsgruppe II des IPCC
8. Das Lambert-Beersche-Gesetz
|
|
|
Trifft elektromagnetische Strahlung auf Materie, so wird ein Teil reflektiert und der andere Teil dringt in die Materie ein. Bei einem Gas wird ein Teil der Strahlung von den Molekülen gestreut und ein Teil von den Molekülen absorbiert und dabei in Wärme umgewandelt. Bei der Durchdringung oder Transmission wird die Strahlungsleistung also vermindert. Der Grad der Verminderung hängt zum einem von der Art des absorbierenden Stoffes ab (Bouguer-Lambertsches Gesetz) und zum anderen von seiner Konzentration (Beersches Gesetz). Die Vereinigung beider Gesetze zum Lambert-Beerschen-Gesetz bildet die Grundlage der modernen Photometrie als analytische Methode.
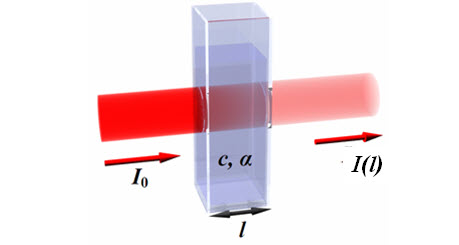
Abb. 8-1: Extinktion eines Lichtstrahls durch eine Küvette der Länge l, (Quelle: Wikipedia Lambert-Beersches-Gesetz)
Die Abnahme der Intensität dI ist proportional zur ortsabhängigen Intensität I(l) der einfallenden Strahlung und zu dem Wegelement dl. Der Weg l ist dabei durch die Richtung der einfallenden Strahlung festgelegt. Somit erhält man:
| $$dI = - \alpha \left( f \right) \cdot c\left( l \right) \cdot I\left( l \right) \cdot dl$$ |
(8.1) |
Der Proportionalitätsfaktor α(f) wird dabei als Absorptionskoeffizient bezeichnet. Er ist bei Molekülen aufgrund ihres inneren Aufbaus frequenzabhängig. Die Konzentration c(l) des durchstrahlten Mediums ist im allgemeinen Fall abhängig vom Ort. Kann man dagegen eine Ortsunabhängigkeit annehmen, so kann (8.1) einfach integriert werden.
| $$\frac{{dI}}{{I\left( l \right)}} = - \alpha \left( f \right) \cdot c \cdot dl$$ |
→ |
$$\int {\frac{{dI}}{{I\left( l \right)}}} = - \alpha \left( f \right) \cdot c \cdot \int {dl} $$ |
→ |
$$\ln \left( {I\left( l \right)} \right) = - \alpha \left( f \right) \cdot c \cdot l + C$$ |
|
| $$I\left( l \right) = I_0 \cdot e^{ - \alpha \left( f \right) \cdot c \cdot l} $$ |
(8.2) |
Die Integrationskonstante C wird durch die Randbedingung I(l=0) = I0 zur Intensität der Strahlung vor Durchdringung des Mediums. Die Schwächung der Strahlung wird also durch eine abfallende e-Funktion beschrieben. Ist die Ortsunabhängigkeit der Konzentration nicht gegeben so muss man (8.2) allgemein schreiben mit:
| $$I\left( l \right) = I_0 \cdot e^{ - \alpha \left( f \right) \cdot \int\limits_0^l {c\left( l \right) \cdot dl} } $$ |
(8.3) |
Der Exponent aus (8.2) wird auch als Extinktion (Auslöschung) bzw. Absorbanz bezeichnet. Graphisch wird (8.2) in Abbildung 8-1 dargestellt. Für die Extinktion E(f) kann man ausgehend von (8.2) schreiben:
| $$E\left( f \right) = - \ln \left( {\frac{I}{{I_0 }}} \right) = - \ln \left( T \right) = \alpha \left( f \right) \cdot c \cdot l$$ |
(8.4) |
Wobei das Verhältnis der austretenden Strahlungsintensität zur einfallenden Strahlungsintensität I/I0 auch als Transmissionsgrad T (bzw. τ) bezeichnet wird.
Die Fläche unter einem definierten Absorptionsprofil wird als Linienstärke S bezeichnet. Sie hängt mit dem Absorptionskoeffizienten a(f) folgendermaßen zusammen:
| $$S = \int\limits_0^\infty {\alpha \left( f \right) \cdot df} $$ |
(8.5) |
Den Absorptionskoeffizienten a(f) kann man auch über die Linienstärke und die so genannte Formfunktion g(f) ausdrücken.
| $$\alpha \left( f \right) = S \cdot g\left( f \right)$$ |
(8.6) |
Wobei die Formfunktion g(f) die normierte Intensitätsverteilung über die Frequenz darstellt. Ihr bestimmtes Integral muss also nach (8.5) und (8.6) den Wert 1 besitzen.
| $$\int\limits_0^\infty {g\left( f \right) \cdot df = 1} $$ |
(8.7) |
Die Formfunktion einer druckverbreiterten Linie lässt sich aus (7.29) bestimmen. Dazu wird als erstes ω durch 2·π·f substituiert und eine Hilfsfunktion z(f)=I(f)/I0 eingeführt:
| $$z(f) = \frac{{\left( {\frac{1}{{4 \cdot \pi \cdot \tau _S }}} \right)^2 }}{{\left( {f - f_0 } \right)^2 + \left( {\frac{1}{{4 \cdot \pi \cdot \tau _S }}} \right)^2 }}$$ |
(8.8) |
Nun muss (8.8) so umgeformt werden, dass die Bedingung (8.7) erfüllt wird. Ein Blick in die Integrationstabelle (Lothar Papula, "Mathematische Formelsammlung für Ingenieure und Naturwissenschaftler", Vieweg & Sohn Verlagsgesellschaft mbH, Braunschweig, 3.Auflage, 1990, S.127) zeigt folgende verwandte Funktion:
| $$\int {\frac{1}{{1 + x^2 }} \cdot dx} = \arctan \left( x \right)$$ |
(8.9) |
Also wird (8.8) auf die Form von (8.9) gebracht:
| $$z(f) = \frac{1}{{\left( {4 \cdot \pi \cdot \tau _S \cdot \left( {f - f_0 } \right)} \right)^2 + 1}}$$ |
(8.10) |
Als nächstes soll (8.10) integriert werden:
| $$Z(f) = \int {\frac{1}{{\left( {4 \cdot \pi \cdot \tau _S \cdot \left( {f - f_0 } \right)} \right)^2 + 1}} \cdot df} $$ |
(8.11) |
Es wird folgende Substitution durchgeführt:
| $$x = 4 \cdot \pi \cdot \tau _S \cdot \left( {f - f_0 } \right)$$ |
→ |
$$\frac{{dx}}{{df}} = 4 \cdot \pi \cdot \tau _S $$ |
→ |
$$df = \frac{{dx}}{{4 \cdot \pi \cdot \tau _S }}$$ |
(8.12) |
Somit wird aus (8.11) und (8.12):
| $$Z(x) = \frac{1}{{4 \cdot \pi \cdot \tau _S }} \cdot \int {\frac{1}{{x^2 + 1}} \cdot dx = } \frac{1}{{4 \cdot \pi \cdot \tau _S }} \cdot \left( {\arctan \left( x \right) + C} \right)$$ |
(8.13) |
In Abbildung 8-2 ist der Graph von arctan(x) dargestellt. Da der Definitionsbereich von –π/2 bis +π/2 läuft und unsere Verteilungsfunktion mit der Frequenz 0Hz beginnen sollte, wird die Integrationskonstante C auf π/2 gesetzt.
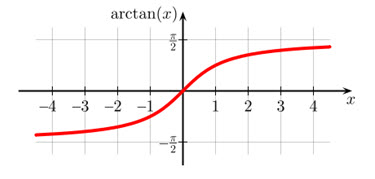
Abb. 8-2: Graph der Funktion arctan(x), (Quelle: Wikipedia Arkustangens)
Macht man nun außerdem die Substitution rückgängig, so wird aus (8.13):
| $$Z(f) = \frac{1}{{4 \cdot \pi \cdot \tau _S }} \cdot \left( {\arctan \left( {4 \cdot \pi \cdot \tau _S \cdot \left( {f - f_0 } \right)} \right) + \frac{\pi }{2}} \right)$$ |
(8.14) |
Damit Z(f) auf einen Definitionsbereich von 0 bis 1 angepasst werden kann, muss (8.14) zuerst mit 4·π·τS multipliziert und dann durch π dividiert werden. Diese Division ist erforderlich, da sich ja der Definitionsbereich durch die Integrationskonstante auf 0 bis π verschoben hat. Es entsteht also die Funktion Z'(f) mit:
| $$Z'(f) = \frac{{4 \cdot \pi \cdot \tau _S }}{\pi } \cdot Z(f) = \frac{1}{\pi } \cdot \left( {\arctan \left( {4 \cdot \pi \cdot \tau _S \cdot \left( {f - f_0 } \right)} \right) + \frac{\pi }{2}} \right)$$ |
(8.15) |
Damit aber Z'(f) das Integral der Formfunktion g(f) werden kann, muss (8.8) mit demselben Faktor aus (8.15) multipliziert werden. Somit wird aus (8.15) und (8.8):
| $$g(f) = \frac{{4 \cdot \pi \cdot \tau _S }}{\pi } \cdot z(f) = \frac{{4 \cdot \pi \cdot \tau _S }}{\pi } \cdot \frac{{\left( {\frac{1}{{4 \cdot \pi \cdot \tau _S }}} \right)^2 }}{{\left( {f - f_0 } \right)^2 + \left( {\frac{1}{{4 \cdot \pi \cdot \tau _S }}} \right)^2 }} = \frac{1}{\pi } \cdot \frac{{\frac{1}{{4 \cdot \pi \cdot \tau _S }}}}{{\left( {f - f_0 } \right)^2 + \left( {\frac{1}{{4 \cdot \pi \cdot \tau _S }}} \right)^2 }}$$ |
(8.16) |
Wegen (7.11) lässt sich (8.16) auch über die Halbwertsbreite Δf½ darstellen:
| $$g(f) = \frac{1}{\pi } \cdot \frac{{\frac{{\Delta f_{1/2} }}{2}}}{{\left( {f - f_0 } \right)^2 + \left( {\frac{{\Delta f_{1/2} }}{2}} \right)^2 }}$$ |
(8.17) |
Mit (8.17) ist die Cauchy-Verteilung entstanden, die allgemein zur Beschreibung von Lorentzkurven in der Spektroskopie und als Breit-Wigner-Verteilung zur Beschreibung von Resonanzkurven Verwendung findet. Die Gleichung (7.29) kann man mit Hilfe der Formfunktion folgendermaßen schreiben:
| $$\hat I(f) = \hat I_0 \cdot \pi \cdot \frac{1}{{4 \cdot \pi \cdot \tau _S }} \cdot g(f) = \frac{{\hat I_0 }}{{4 \cdot \tau _S }} \cdot g(f)$$ |
(8.18) |
In (8.4) wurde der Transmissionsgrad T als das Verhältnis der aus dem Medium austretenden Strahlungsintensität zur in das Medium eintretenden Strahlungsintensität I/I0 eingeführt. Der Teil, eingestrahlten Intensität, die im Medium verbleibt, wird als Absorption bezeichnet. Da der Transmissionsgrad ein Verhältnis ist, das sich zwischen 0 und 1 bewegt, wird das Gegenstück auch als prozentuale Absorption A bezeichnet. Sie ist genau wie der Transmissionsgrad frequenzabhängig. Man kann also folgende Beziehung aufstellen:
| $$A\left( f \right) = 1 - T\left( f \right) = 1 - \frac{{I\left( f \right)}}{{I_0 }}$$ |
(8.19) |
Setzt man das Lambert-Beersche-Gesetz nach (8.2) in (8.19) ein und drückt nach (8.6) den Absorptionskoeffizienten a(f) durch die Formfunktion g(f) aus, so erhält man:
| $$A\left( f \right) = 1 - e^{ - S \cdot g\left( f \right) \cdot c \cdot l} $$ |
(8.20) |
Eine Reihenentwicklung der e-Funktion liefert (Lothar Papula, "Mathematische Formelsammlung für Ingenieure und Naturwissenschaftler", Vieweg & Sohn Verlagsgesellschaft mbH, Braunschweig, 3.Auflage, 1990, S.156):
| $$A\left( f \right) = 1 - \left( {1 - \frac{{S \cdot g\left( f \right) \cdot c \cdot l}}{1} + \frac{{\left( {S \cdot g\left( f \right) \cdot c \cdot l} \right)^2 }}{2} - \frac{{\left( {S \cdot g\left( f \right) \cdot c \cdot l} \right)^3 }}{6} + ...} \right)$$ |
(8.21) |
Ist der Exponent der e-Funktion S·g(f)·c·l sehr viel kleiner als 1, so können die Terme höherer Ordnung vernachlässigt werden und (8.21) vereinfacht sich zu:
| $$A\left( f \right) = S \cdot g\left( f \right) \cdot c \cdot l$$ |
(8.22) |
Damit ist das Absorptionsprofil für hinreichend kleine prozentuale bzw. relative Absorption direkt proportional zum Linienprofil. Das heißt, dass sich die Frequenzverteilung direkt im aufgenommenen Spektrum widerspiegelt. Mit zunehmender Absorption (z.B. durch steigende Weglänge oder steigende Konzentration) ist die Proportionalität zwischen Linienprofil und Absorptionsprofil nicht mehr gegeben. Während die Linienränder noch linear abgebildet werden, wird das Linienzentrum durch den wachsenden Einfluss der e-Funktion zunehmend verzerrt. Das Ergebnis ist eine Abflachung der Linie bei gleichzeitiger scheinbarer Zunahme der Halbwertsbreite. Zur Berechnung der Halbwertsbreite wird von (8.20) ausgegangen. Die prozentuale Absorption im Linienzentrum wird zu A0 gesetzt. Dann gilt für die Absorption bei der Hälfte des Maximums:
| $$A\left( {f_{1/2}^/ } \right) = \frac{{A_0 }}{2}$$ |
(8.23) |
Einsetzen von (8.23) in (8.20) liefert den Zusammenhang zwischen Linienprofil und Absorption:
| $$\frac{{A_0 }}{2} = 1 - e^{ - S \cdot g\left( {f_{1/2}^/ } \right) \cdot c \cdot l} $$ |
→ |
$$e^{ - S \cdot g\left( {f_{1/2}^/ } \right) \cdot c \cdot l} = 1 - \frac{{A_0 }}{2}$$ |
→ |
$$ - S \cdot g\left( {f_{1/2}^/ } \right) \cdot c \cdot l = \ln \left( {1 - \frac{{A_0 }}{2}} \right)$$ |
|
| $$g\left( {f_{1/2}^/ } \right) = - \frac{1}{{S \cdot c \cdot l}} \cdot \ln \left( {1 - \frac{{A_0 }}{2}} \right)$$ |
(8.24) |
In (8.24) wird nun die Formfunktion nach (8.17) eingesetzt. Dabei wird die neue, sich aus dem Absorptionsprofil ergebende Halbwertsbreite mit Δf½' bezeichnet. Es gilt damit:
| $$\frac{1}{\pi } \cdot \frac{{\frac{{\Delta f_{1/2} }}{2}}}{{\left( {\frac{{\Delta f_{1/2}^/ }}{2}} \right)^2 + \left( {\frac{{\Delta f_{1/2} }}{2}} \right)^2 }} = - \frac{1}{{S \cdot c \cdot l}} \cdot \ln \left( {1 - \frac{{A_0 }}{2}} \right)$$ |
mit |
$$\Delta f_{1/2}^/ = 2 \cdot \left| {f_{1/2}^/ - f_0 } \right|$$ |
(8.25) |
| $$\frac{2}{\pi } \cdot \frac{{\Delta f_{1/2} }}{{\Delta f_{1/2}^{/2} + \Delta f_{1/2} ^2 }} = - \frac{1}{{S \cdot c \cdot l}} \cdot \ln \left( {1 - \frac{{A_0 }}{2}} \right)$$ |
→ |
$$\frac{{\Delta f_{1/2} }}{{\Delta f_{1/2}^{/2} + \Delta f_{1/2} ^2 }} = - \frac{\pi }{{2 \cdot S \cdot c \cdot l}} \cdot \ln \left( {1 - \frac{{A_0 }}{2}} \right)$$ |
|
| $$\Delta f_{1/2}^/ = \sqrt { - \frac{{\Delta f_{1/2} }}{{\frac{\pi }{{2 \cdot S \cdot c \cdot l}} \cdot \ln \left( {1 - \frac{{A_0 }}{2}} \right)}} - \Delta f_{1/2} ^2 } $$ |
→ |
$$\Delta f_{1/2}^/ = \Delta f_{1/2} \cdot \sqrt { - \frac{{2 \cdot S \cdot c \cdot l}}{{\pi \cdot \Delta f_{1/2} \cdot \ln \left( {1 - \frac{{A_0 }}{2}} \right)}} - 1} $$ |
(8.26) |
Aus (8.17) wird g(f0) bestimmt:
| $$g(f_0 ) = \frac{1}{\pi } \cdot \frac{{\frac{{\Delta f_{1/2} }}{2}}}{{\left( {\frac{{\Delta f_{1/2} }}{2}} \right)^2 }} = \frac{1}{\pi } \cdot \frac{1}{{\frac{{\Delta f_{1/2} }}{2}}} = \frac{2}{\pi } \cdot \frac{1}{{\Delta f_{1/2} }}$$ |
(8.27) |
Nun wird (8.27) in (8.20) eingesetzt, um A0 zu bestimmen:
| $$A_0 = 1 - e^{ - \frac{{S \cdot 2 \cdot c \cdot l}}{{\pi \cdot \Delta f_{1/2} }}} $$ |
(8.28) |
Nun wird (8.28) nach dem Exponenten umgeformt:
| $$e^{ - \frac{{S \cdot 2 \cdot c \cdot l}}{{\pi \cdot \Delta f_{1/2} }}} = 1 - A_0 $$ |
→ |
$$\frac{{2 \cdot S \cdot c \cdot l}}{{\pi \cdot \Delta f_{1/2} }} = - \ln \left( {1 - A_0 } \right)$$ |
(8.29) |
Nun kann (8.29) in (8.26) eingesetzt werden:
| $$\Delta f_{1/2}^/ = \Delta f_{1/2} \cdot f\left( {A_0 } \right) = \Delta f_{1/2} \cdot \sqrt {\frac{{\ln \left( {1 - A_0 } \right)}}{{\ln \left( {1 - \frac{{A_0 }}{2}} \right)}} - 1} $$ |
(8.30) |
In Abbildung 8-3 ist die Verbreiterungsfunktion f(A0) nach (8.30) in Abhängigkeit von der prozentualen Absorption im Linienzentrum A0 dargestellt. Das heißt, je mehr sich die prozentuale Absorption im Linienzentrum 100% nähert, desto mehr "zerfließt" die Spektrallinie.
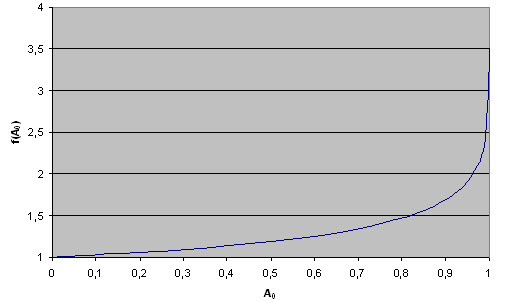
Abb. 8-3: Linienverbreiterung durch prozentuale Absorption
|



